Na figura abaixo uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas acima da reta .
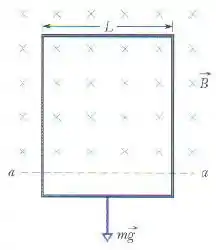
Deixa-se cair a espira, que acelera sob a ação da gravidade até atingir uma certa velocidade terminal . Escreva uma expressão para , ignorando a resistência do ar.
Passo 1
Quando a espira atinge a velocidade terminal , a velocidade passa a ser constante e a força resultante sobre a espira é nula.
Para que isso seja verdade, é necessário que a força magnética sobre a espira seja igual ao peso da mesma, certo?
Logo:
Assim, a corrente induzida na espira será:
Beleza, agora precisamos nos resolver com essa corrente.
Passo 2
A corrente induzida na espira será dada por:
Para esse tipo de problema, sabemos que a induzida será dada por:
Portanto:
Passo 3
Igualando as expressões dos passos 1 e 2, teremos:
Organizando esses caras, teremos: