Força e Torque sobre uma Espira, Lei de Faraday, Lei de Lenz
A figura abaixo mostra uma barra condutora de comprimento , deslizando para a direita, com velocidade constante , em contato com um fio, de modo a formar um circuito de resistência . Também está ilustrado na figura um campo magnético , constante e uniforme, saindo da página.
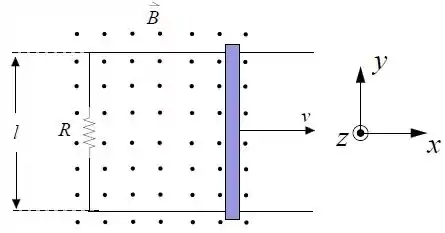
Determine o sentido da corrente induzida no circuito (horário ou anti-horário), justificando sua resposta.
Calcule a corrente induzida .
Calcule o vetor força externa que está sendo aplicada na barra de modo a manter sua velocidade constante.
Passo 1
Determine o sentido da corrente induzida no circuito (horário ou anti-horário), justificando sua resposta.
A Lei de Lenz diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Mas basicamente o que nós precisamos tirar disso é que:
Se o fluxo do campo magnético está aumentando, o campo induzido tenta atrapalhar ele (corrente no sentido horário). Se o fluxo está diminuindo, o campo induzido tenta ajudar ele (corrente no sentido anti-horário).
Ok! O fluxo do campo magnético é dado por (no caso de um campo magnético uniforme):
O campo magnético é constante e está saindo da folha, portanto, ele é positivo.
Como a área está aumentando, isso faz com que a variação da área com o tempo seja positiva:
Logo:
Opa! Como o fluxo do campo magnético está aumentando, a corrente estará no sentido horário.
Passo 2
Calcule a corrente induzida .
A corrente será dada por:
Então, o nosso trabalho aqui é calculando a induzida na espira.
De acordo com a Lei de Faraday:
Onde é o fluxo magnético na espira que, para um campo magnético uniforme e constante, é dado por:
Onde .
Portanto:
Assim, a corrente induzida será dada por:
Passo 3
Calcule o vetor força externa que está sendo aplicada na barra de modo a manter sua velocidade constante.
Para que a velocidade da barra seja constante, a força resultante sobre ela deve ser nula. Portanto:
Assim, temos que calcular a força magnética sobre a barra.
Para uma barra retilínea, conduzindo corrente , a força magnética será dada por:
Onde tem o módulo igual ao comprimento da barra e a mesma direção e sentido da corrente. Assim, como a corrente está no sentido horário:
Como o campo magnético está saindo da página, . Portanto:
Sabendo que:
Então:
Finalmente, a força que deve ser exercida sobre a barra para que esta permaneça com velocidade constante é:
Resposta
A corrente estará no sentido horário.