Uma espira condutora retangular , rígida, de comprimento e largura está sujeita a um campo magnético estacionário, mas não uniforme, perpendicular ao seu plano, tal que , onde são coordenadas cilíndricas, os correspondentes vetores unitários, conforme indicados na figura, e . O lado da espira, mais próximo ao eixo , está a uma distância desse. A espira constitui-se de um material ôhmico e sua resistência total é igual a , ao passo que a sua autoindutância é desprezível.
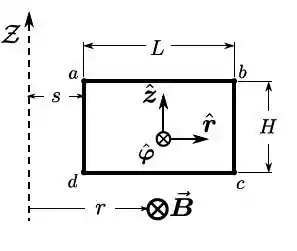
- Determine o módulo do fluxo do campo magnético que atravessa a região plana interior da espira.
- Determine, com justificativa detalhada, no caso de a espira estar em repouso, se alguma corrente induzida circula ao longo da espira e, se for o caso, indique claramente o seu sentido e calcule o seu módulo.
- Considere agora que a espira se desloca para a direita a uma velocidade de módulo constante . Nessa nova situação, determine novamente, com justificativa detalhada, se alguma corrente induzida circula ao longo da espira e, se for o caso, indique claramente o seu sentido e calcule o seu módulo.
Passo 1
Vamos calcular o fluxo como pedido:
Para tal, precisamos encontrar o campo magnético. Felizmente ele foi dado pelo enunciado:
Arbitrando nosso vetor área para ficar no mesmo sentido do campo:
Passo 2
Fazendo o cálculo do fluxo:
Arrumando e puxando constante para fora:
Agora, como nossa região de integração é um retângulo, a boa é usar coordenadas cartesianas, portanto:
Passo 3
Além disso nossa região de integração é o quadrilátero:
Onde esse é um ponto arbitrário onde está a base do retângulo (você poderia ter arbitrado como zero que ninguém se importaria). Plugando na integral, podemos separar elas:
Resolvemos:
Passo 4
Agora temos que justificar detalhadamente se passa alguma corrente induzida na espira. Bom, isso é trabalho para a Lei de Faraday:
Juntando ela com a Lei de Ohm:
E temos nossa corrente induzida:
Passo 5
Agora falta resolver essa derivada com respeito ao tempo. No caso da espira estar em repouso, temos que tudo é constante, logo:
Sendo todas as letras constantes... Só nos resta concluir que a derivada é zero:
Portanto não. Não existe corrente induzida:
Passo 6
Agora considerando que a espira se desloca para a direita à uma velocidade constante:
Podemos brincar de fazer derivadas. Pelo mesmo argumento de antes:
Encontramos a derivada do fluxo:
Puxando constantes pra fora:
Passo 7
A derivada de um log com razão no meio é mais facilmente calculada se expandirmos como diferença de logs:
Pela regra da cadeia:
Substituindo :
Arrumamos tudo (eu tenho toc):
Passo 8
Por fim, temos que a corrente induzida é:
Lindo! #SQN... Agora precisamos encontrar o sentido da corrente, já temos seu módulo. Encontramos o sentido por dois jeitos:
- Pela nossa arbitragem do vetor área;
- Pela Lei de Lenz.
Normalmente a banca pede o segundo jeito, mas eu prefiro o primeiro. Como arbitramos:
Isto significa que, pela regra da mão direita, se colocar seu polegar (eu vinha falando “nosso” polegar nas outras questões!? Nós não compartilhamos polegares aqui no Responde Aí) no sentido do vetor área, os outros dedos dão o sentido positivo da corrente. Ou seja, neste caso o sentido positivo é o horário. Como a corrente que encontramos é positiva, ela está no sentido horário também.
Passo 9
Alternativamente podemos fazer pela Lei de Lenz (como ele não exigiu isto no enunciado acho que não teria problema fazer da outra forma, mas enfim).
Como a espira está se afastando, o campo magnético é cada vez menor e portando o fluxo está diminuindo. O fluxo é proveniente de um campo entrando na página, portanto a corrente induzida tenta compensar essa diminuição fazendo o campo entrar também. Logo, pela regra da mão direita o sentido da corrente vai ser horário. Eu acho detestável essa solução, mas tem gosto pra tudo...
Resposta
a)
b)
c)
Sentido horário.