Uma bobina retangular de voltas e lados e está totalmente imersa numa região de campo magnético homogêneo de intensidade . Ela gira com relação a um eixo perpendicular ao campo magnético e perpendicular a um de seus lados com uma velocidade angular de , como mostra a figura. Os extremos da espira é acoplado a uma resistência de .
- Em qual posição da espira a corrente assume seu valor máximo? Justifique.
- Qual o valor da induzida máxima?
- Qual o valor e o sentido da corrente na primenta vez que atinge seu valor máximo, a partir da posição da figura.
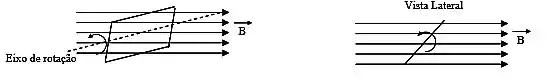
Passo 1
Sabemos que a corrente será máxima quando a fem induzida assumir seu valor máximo.
E esta assume o valor máximo quando a variação do fluxo é máxima, certo? E quando isso acontece? Quando o fluxo é zero.
Obs.: Para entender melhor, a derivada do campo em relação ao tempo (variação do fluxo) assume seu valor máximo nos vértices do gráfico que tem a forma senoidal. E nestes vértices, não ocorre fluxo de campo magnético.
Qual a condição para o fluxo ser zero no caso da posição da espira e do campo magnético? O vetor área da espira deve estar perpendicular ao campo magnético. Ou seja, o plano da espira deve estar paralelo ao campo magnético.
Passo 2
Para calcular a fem induzida, calculamos o fluxo e a derivada.
Então,
A fem será máxima quando , logo::
Passo 3
Sabemos os valores necessários, basta aplicar a fórmula:
Pela regra da mão direita, a corrente está saindo da folha.
Resposta
- Quando o plano da espira deve estar paralelo ao campo magnético..
- , para fora da folha.