Uma espira condutora, quadrada, de lado está incialmente paralela ao plano de um sistema de coordenadas. Ela está imersa em uma região onde há um campo magnético uniforme e estacionário dado por . Considere, agora, três possíveis movimentos distintos para a espira:
- A espira é solta e cai em queda livre ao longo do eixo , permanecendo paralela ao plano
- A espira gira em torno de um eixo perpendicular a seu plano e que passa pelo seu centro.
- A espira gira em torno de um eixo que passa por um de seus lados.
Em quais dessas situações haverá uma corrente induzida na espira?
- Nenhuma delas
Passo 1
Para entendermos bem o que está envolvido nos itens dessa questão, vamos utilizar a figura abaixo. Na direção , temos o campo magnético, que é o mesmo em todos os pontos do espaço e não varia com o tempo, por isso é uniforme e estacionário.
Temos uma espira condutora quadrada (cuja área não varia com o tempo) que está totalmente inserida na região de campo magnético e é paralela ao plano , como desenhamos na figura abaixo.
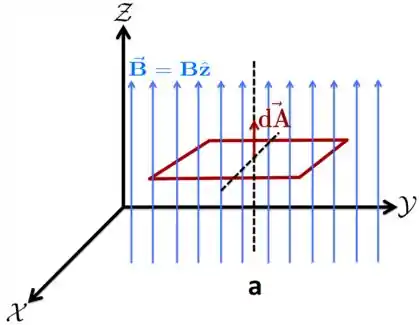
Na Figura a, temos dois eixos passando pela espira, um que é paralelo ao eixo , portanto, perpendicular à sua superfície, e outro paralelo ao eixo passando por um dos lados da espira.
Se a espira, que está totalmente inserida no campo magnético na Figura , cai em queda livre, o fluxo magnético não varia com o tempo, já que seu vetor área está sempre paralelo ao vetor do campo magnético que é constante e uniforme em toda a região. Existe fluxo magnético, porém o mesmo não varia com o tempo!!
Cuidado: não é porque a espira está acelerada em queda livre que o fluxo varia com o tempo. Apesar de sua velocidade variar com o tempo, o produto escalar permanece o mesmo em todo o tempo durante a queda da espira!
Por outro lado, se a espira gira em torno do eixo perpendicular à sua superfície, representado na Figura a, novamente o fluxo permanece o mesmo com o tempo já que, de novo, permanece o mesmo em todo o tempo, independentemente de quão rápido essa espira gira em torno do eixo perpendicular à sua superfície.
Portanto, os itens e estão INCORRETOS.
Passo 2
Agora, suponha que a espira seja girada em torno do eixo paralelo ao eixo da Figura a e, como resultado, obtemos a sua nova posição representada na Figura b abaixo.
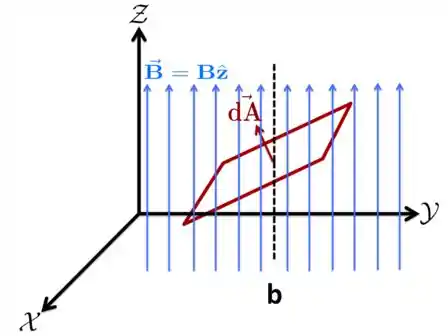
Diferente do caso da Figura a, o vetor nessa nova situação faz um ângulo variável como tempo com o vetor . Apesar de a área da espira permanecer a mesma e o campo magnético também, agora o produto escalar
que entrará no cálculo do fluxo magnético, varia com o tempo, uma vez que o ângulo entre e varia com o tempo.
Portanto, nessa situação haverá uma fem induzida na espira e, como ela é condutora, haverá uma corrente induzida como resultado.
Isso torna o item da questão CORRETO.
Sugestão: procure sempre, em problemas desse tipo, reconhecer as características do campo, bem como as do objeto em questão dentro desse campo: “condutor ou não?”, “Mesma área em todo o tempo?”, “O ângulo entre o campo magnético e a área do objeto é sempre o mesmo?” Rastrear essas características é muito é importante!!
Resposta
Portanto, a resposta correta é a letra a) .