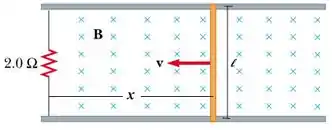
Uma barra condutora de comprimento desliza sem atrito sobre duas barras condutoras e paralelas (veja a figura abaixo). Um resistor está conectado como mostrado na figura. Um campo magnético constante está aplicado perpendicularmente à página. Um agente externo transporta a barra com velocidade . Qual o valor e o sentido da corrente que circula no circuito (ou seja, que atravessa o resistor de )?
(a) no sentido anti-horário.
(b) no sentido horário.
(c) no sentido anti-horário.
(d) no sentido horário.
(e) no sentido anti-horário.
Passo 1
Vamos, inicialmente, calcular o fluxo magnético através do circuito. Para isso, escolhemos o vetor área entrando no plano da página. Temos, então, .
Passo 2
Bem, a fem induzida no circuito é dada por:
Temos e precisamos calcular , certo?
Passo 3
Vamos lá: a barra se movimenta com uma velocidade constante para a esquerda. Em um intervalo de tempo , seu deslocamento será para a esquerda.
Logo, a área será dada por:
onde é a área no instante , antes da barra começar a se movimentar.
E, portanto, a fem induzida será:
Passo 4
Por fim, para o cálculo da corrente induzida, fazemos:
Notem que a corrente é positiva! Vamos ver o que isso significa:
- Pela lei de Lenz, sabemos que o sistema irá induzir uma corrente de forma a cancelar a variação do fluxo magnético e encontrar um equilíbrio;
- Como a área está diminuindo, o fluxo também diminui;
- Assim sendo, o equilíbrio se dá com o aumento do fluxo: campo magnético induzido no mesmo sentido do original;
- Pela regra da mão direita, a corrente circula no sentido horário .
Resposta
(d) no sentido horário.