Q - Uma corrente constante passa por um fio infinito conforme a figura. Um loop retangular está localizado ao lado e no mesmo plano do fio.

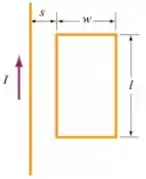
Calcule o fluxo magnético através do loop retangular. Existe uma fem induzida nesse caso? Por quê?

Suponha agora que a corrente depende do tempo como , onde e são constantes positivas. Qual será a fem induzida e qual o sentido da corrente induzida no loop retangular? Justifique suas respostas.

Começando com o item , temos que o fluxo é encontrado com:

Onde o elemento é o elemento de área da espira. Como o campo varia com a distância perpendicular ao fio infinito o elemento de área por onde passo o campo vai ser dado por .

Onde .

Como o campo é paralelo ao elemento de área, temos que:

Substituindo com o que sabemos, temos:

Assim temos que:

Agora se tomarmos a derivada desse fluxo com relação ao tempo temos que:

Logo , então não temos fem induzida, já que a variação temporal do fluxo é zero.

Agora para o item , temos que todo o processo que fizemos antes para o cálculo do fluxo é o mesmo, só que a gora temos uma corrente , assim temos que:

Agora vamos calcular a derivada do fluxo em relação ao tempo, assim:

Como variação do fluxo é positiva temos um aumento do fluxo do campo com o tempo. A fem induzida vai ser igual a:

Como o fluxo aumenta com o tempo então surge uma corrente induzida no sentido anti-horário que gera um campo para fora do plano da folha com a intenção de diminuir o fluxo do campo.