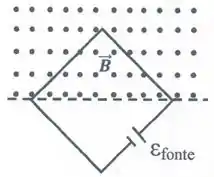
Uma espira quadrada com de lado é mantida perpendicular a um campo magnético uniforme com metade de sua área na região de campo, como mostra a figura. O módulo do campo magnético está variando de acordo com a equação , com em Tesla e em segundos. Ligada à espira, temos uma fonte de força eletromotriz (f.e.m.) com . Determine o valor da força eletromotriz total aplicada à espira o sentido da corrente em torno dela.
(a) , no sentido horário.
(b) , no sentido horário.
(c) , no sentido anti-horário.
(d) , no sentido anti-horário.
(e) , no sentido horário.
Passo 1
Bem, vamos analisar o problema por partes:
- Pela expressão do módulo de , sabemos que ele diminui. Sendo assim, pela Lei de Lenz, a corrente induzida se opõe a essa diminuição.
- Isso significa que a corrente induzida tem sentido anti-horário.
- A fem induzida é dada por (lembrando que somente a área em contato com o campo magnético é considerada para o cálculo da fem!):
- Logo, a fem total será dada por:
Resposta
(d) , no sentido anti-horário.
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v