Considere uma espira circular, flexível e condutora de raio variável no tempo , imersa em um campo magnético uniforme, perpendicular ao seu plano. Para manter uma força eletromotriz variando linearmente com o tempo , o seu raio deveria variar de acordo com (onde é uma constante):
Passo 1
O primeiro passo aqui, galera, é identificar o assunto da questão. Discutindo, rapidão, o enunciado, a gente tem o seguinte:
- Uma espira circular e condutora, por isso é fácil medir uma corrente que eventualmente passe por ela;
- Além disso, essa espira, que tem o raio variável (por isso flexível!), delimita uma área variável;
- Um campo magnético, que é o mesmo em todo os pontos do espaço em todo o tempo, ou seja, uniforme e constante.
Então, já sacou, né? Um vetor passando por uma área, logo vem na cabeça a ideia de fluxo e, no caso, de fluxo magnético:
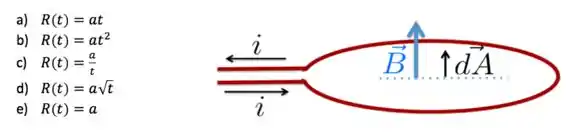
em que é área da espira é a direção do vetor área perpendicular à superfície. Como tem um produto escalar aí na expressão, a gente precisa definir bem a direção dos vetores e . Vamos colocar, por exemplo, como está na figura: os dois paralelos apontando para cima.
Passo 2
Bom, agora, se tem força eletromotriz, então deve haver variação do fluxo magnético com o tempo. Mas, olha bem para espira: o campo é sempre o mesmo em todo lugar o todo tempo todo, ou seja, ele é uniforme e constante e a espira não está girando. Então, o que é que tá fazendo o fluxo variar no tempo? O raio e, portanto, a área da espira é que vai variar no tempo!
Como o campo é constante, e colocando o elemento de área apontando na mesma direção de como na figura, o fluxo fica escrito como:
Passo 3
Agora que já sabemos o fluxo, derivamos em relação ao tempo (lembrando da regra da cadeia!), para obter (tomando apenas o módulo da força eletromotriz):
Passo 4
Para que varie linearmente com o tempo, como pede a questão, devemos derivar e multiplicar por ele mesmo (aproveita para dar uma olhada verificar isso na equação do Passo 3!) e obter o comportamento de uma reta. Portanto, o próprio raio deve ser uma função linear do tempo:
.
Resposta
Derivando o raio (resposta da letra a) e substituindo em , temos
que varia linearmente com o tempo , como pedido na questão.