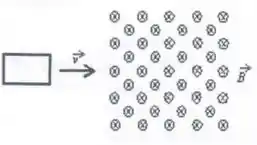
Uma espira quadrada se move com uma velocidade constante de uma região livre de campo para uma região de campo uniforme, como mostrado. Qual dos cinco gráficos mostra corretamente a corrente induzida no circuito em função do tempo ?
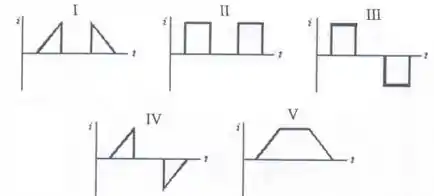
(a) I.
(b) II.
(c) III.
(d) IV.
(e) V.
Passo 1
Sabemos que a fem induzida pode ser calculada como
Vamos dividir o problema em três partes. Na primeira, a espira está entrando na região de campo magnético. Como o campo é constante e a área é dada por , temos, para essa região:
Como a fem é constante, a corrente também será.
Passo 2
A segunda parte é quando a espira está dentro da região de campo magnético. Como a velocidade é constante, a variação de fluxo será constante e, portanto, a fem induzida será nula.
Assim sendo, neste trecho, a corrente é nula.
Passo 3
Na terceira parte, a espira está saindo da região de campo magnético. Isso significa que, agora, a área irá diminuir. Temos que
onde é a área total da espira.
A fem induzida será dada, portanto, por:
Agora, a fem induzida inverte de sinal se comparada à fem obtida na parte 1. Isso significa que a corrente também se inverte!
Logo, o gráfico que representa corretamente a variação da corrente induzida em função do tempo é o III.
Resposta
(c) III.