Uma espira de de raio e uma resistência de é submetida a um campo magnético uniforme cujo módulo varia de acordo com a figura abaixo.
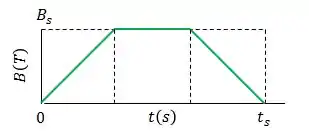
A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .
O plano da espira é perpendicular a . Determine a força eletromotriz induzida na espira durante os intervalos de tempo:
;
;
;
Passo 1
A espira tem área fixa e o seu plano é perpendicular ao campo magnético . Nesse caso, a induzida será dada por:
Onde:
Além disso, nesse gráfico, podemos ver que em alguns trechos, o campo magnético varia linearmente. Dessa forma, podemos dizer que:
Logo:
Beleza, agora só temos que aplicar isso em cada caso.
Passo 2
;
Aplicando a relação acima a esse caso, teremos:
Passo 3
;
Nesse intervalo, o campo magnético é constante, logo:
Passo 4
;
Resposta