Dois trilhos paralelos condutores de resistência desprezível distam e são ligados por um resistor de . O circuito também contém uma barra de metal com resistência de , deslizando sobre os trilhos com velocidade constante de . Um campo magnético uniforme de é aplicado perpendicularmente ao plano dos trilhos, conforme figura.
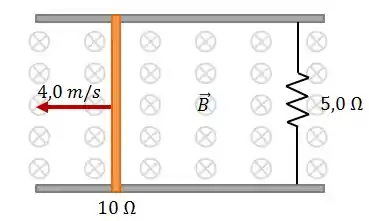
Calcule:
O valor e o sentido da corrente na barra;
O vetor força magnética que atua sobre ela;
A potência total dissipada no circuito;
Passo 1
O valor e o sentido da corrente na barra;
Pra calcularmos a corrente na barra, precisamos começar calculando a induzida que aparece no circuito.
Esse induzida é dada a partir da Lei de Faraday:
Onde . Sendo a distância entre os dois trilhos.
Logo:
Para os cálculos, nos interessa somente o módulo da induzida, logo:
Passo 2
Assim, o valor da corrente será dado por:
Como os resistores estão em série, a resistência equivalente será a soma das resistências. Assim, substituindo os valores, teremos:
Passo 3
O sentido da corrente induzida é determinado pela Lei de Lenz, que diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
É o seguinte... se o fluxo magnético está aumentando, a corrente induzida gerará um campo magnético no sentido contrário ao fluxo (nesse caso, sentido anti-horário). Se o fluxo magnético está diminuindo, a corrente induzida gerará um campo magnético no mesmo sentido do fluxo (nesse caso, sentido horário).
Aqui, como o campo magnético é uniforme e constante e a área da espira está aumentando, o fluxo magnético está aumentando, logo, a corrente induzida está no sentido anti-horário.
Passo 4
O vetor força magnética que atua sobre ela;
A força magnética sobre um condutor retilíneo é dada por:
Onde tem a direção e sentido da corrente.
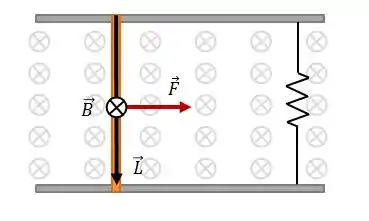
Passo 5
A potência total dissipada no circuito;
A potência dissipada no circuito é dada por:
Resposta
A corrente induzida está no sentido anti-horário.