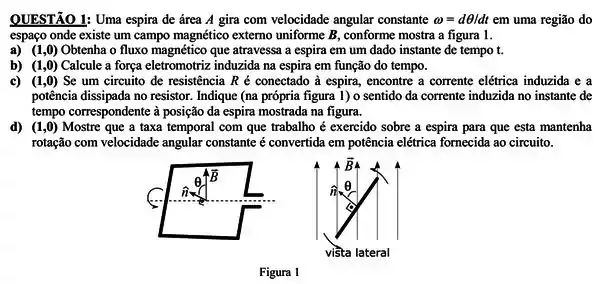
Passo 1
Letra (a). O fluxo magnético é dado por:
Mas, é uma função do tempo. Ou seja: pois a espira gira com velocidade angular constante. Dessa forma:
Passo 2
Letra (b). Pela lei de Faraday, é a variação desse fluxo que vai determinar a força eletromotriz induzida:
Passo 3
Letra (c). A corrente induzida vale:
Essa corrente gera uma potência igual a , ou seja:
A lei de Lenz diz que a variação de fluxo magnético gera uma corrente que tende a minimizar essa variação de fluxo magnético. Pela regra da mão direita, uma corrente no sentido anti-horário tende a gerar um campo que se opõe à variação do fluxo.
É por isso que existe um sinal de menos na equação da lei de Faraday (e é esse menos que nos faz chamar essa lei de lei de Faraday-Lenz).
Passo 4
Letra (d). Para acertar essa parte precisamos nos lembrar do momento dipolo magnético. O momento dipolo magnético multiplicado pelo campo é igual ao trabalho. Essa multiplicação é escalar, na seguinte forma:
Onde o dipolo magnético é expresso por:
Então, esse produto vai dar:
A taxa de variação desse trabalho em relação ao tempo vale:
Será que isso é igual à potência elétrica do circuito?
Passo 5
Letra (d). Continuação. Vamos ver:
Então, a resposta é sim, temos potências de módulos iguais. Isso mostra que a energia é, realmente, transferida da taxa de variação do trabalho para o circuito!
Resposta
Letra (a)
Letra (b)
Letra (c)