Passo 1
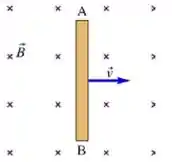
Não temos exatamente uma espira, mas a gente pode aplicar a lei de Faraday nessa situação de um jeito um pouco diferente: a gente calcula fluxo pela área varrida pela barra em movimento. Isso vai dizer o quanto de potencial vai se concentrar nas pontas da barra:
A área é a de um retângulo com comprimento igual ao da barra e largura igual ao que a barra percorre durante o instante de tempo , ou seja: um retângulo de dimensões e . Assim:
Passo 2
É a derivada desse fluxo magnético que, pela lei de Faraday, vai dar a DDP na barra:
Resposta
Letra (e).
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v