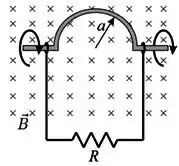
A figura abaixo mostra uma semi-circunferência de raio que gira com revoluções por segundo na presença de um campo magnético uniforme de . Sendo , determine a amplitude da corrente induzida no circuito.
(a) .
(b) .
(c) .
(d) .
(e) .
Passo 1
Vamos calcular, inicialmente, o fluxo magnético . Temos:
Aqui, chamamos de a área constante do circuito e , a área da semi-circunferência. O ângulo entre e a área é dado por .
Temos, então:
Passo 2
A fem induzida será dada por:
Logo, a corrente induzida será dada por:
Sua amplitude será:
Resposta
(c) .
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v