Uma barra de comprimento e resistência move-se com velocidade ao longo de trilhos horizontais condutores ideais (sem resistência) e sem atrito, conforme figura abaixo.

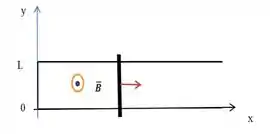
Supondo que , com , calcule a corrente induzida no circuito e a sua direção se e em temos .

Existe algum instante de tempo em que a corrente induzida seja zero? Se sim, qual? (justifique as suas afirmações).

Supondo que , calcule a corrente induzida no circuito indicando seu sentido em cada quadrante de , isto é, em se a posição da barra é dada por .

Podemos ver, pela equação da corrente que todas as constantes, inclusive a exponencial serão sempre não nulos, nesse caso, a corrente somente se anulará quando:

Para resolver esse item, vamos fazer o mesmo mimimi que fizemos no item só que agora, temos e , vamos começar com a Lei de Faraday:

Vamos primeiro calcular o fluxo , se liga!

Arbitrando o vetor área no mesmo sentido do campo magnético, temos:

Sendo a área , substituindo o fluxo na equação da Lei de Faraday, temos:

Vamos agora calcular a derivada, se liga:

Para a corrente, temos:

Como arbitramos o vetor área paralelo ao vetor campo, temos que o sentido da corrente será horário nos intervalos e anti-horário nos intervalos .