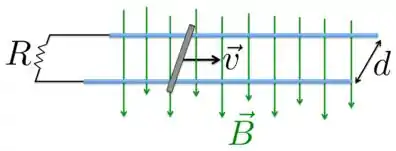
Trilhos paralelos condutores estão dispostos horizontalmente, distando um do outro, e são unidos por um resistor . Este aparato está em uma região onde há um campo magnético constante e uniforme, vertical e orientado para baixo. Uma barra condutora é puxada para a direita, sobre os trilhos sem atrito, com velocidade constante . A intensidade da corrente induzida é dada por
Passo 1
Precisamos ver aqui, antes de mais nada, o que está acontecendo com o fluxo do campo magnético à medida que a barra condutora é puxada para a direita.
Primeiro, a área por onde está passando o campo magnético está aumentando com o tempo e mais linhas de campo estão atravessando essa área. Por isso, o fluxo magnético também está aumentando com o tempo, o que vai dar origem a uma corrente induzida. O campo produzido por essa corrente, vai se opor à variação desse fluxo magnético.
Agora vamos colocar isso em termos de conta e encontrar que valor essa corrente induzida tem.
Passo 2
Como já vimos, o fluxo magnético é dado por:
Para vermos como fica o produto escalar dentro dessa integral, precisamos escolher qual sentido e direção da vetor área . Vamos colocar esse vetor paralelo a , como na figura abaixo.
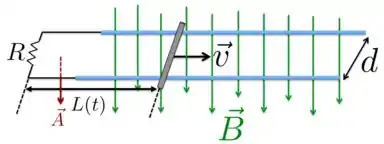
Nesse caso, se o campo magnético é uniforme, ou seja, se ele tem o mesmo valor em todos os pontos da região, então a integral se simplifica para
Como já indicamos na expressão acima e já discutimos no Passo 1, é a área varia que com o tempo à medida que a barra condutora se desloca para a direita.
Olhando para a figura acima, a gente vê que é o comprimento que varia com o tempo. Portanto: .
Passo 3
Tendo o fluxo magnético e entendendo porque ele varia com o tempo, podemos encontrar o valor da corrente induzida.
O módulo da fem induzida é dado por
Como é exatamente a velocidade da barra condutora e , então:
Resposta
Letra b.