. Uma barra condutora fina se move com velocidade constante sobre um par de trilhos condutores finos, como mostrado na figura abaixo. O trecho em que os trilhos estão angulados tem um comprimento horizontal e a separação entre os trilhos no trecho em que eles são paralelos vale . No instante , a barra se encontra no ponto onde os trilhos se encontram. O atrito entre os trilhos e a barra é desprezível e todo o sistema está imerso em uma região de campo magnético constante .

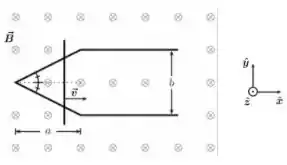
Determine o módulo do fluxo de campo magnético através da área definida pelos trilhos e a barra como função do tempo , considerando os intervalos e . Sugestão: Para o intervalo , utilize uma semelhança de triângulos para obter uma relação entre a porção de comprimento da barra dentro do circuito e o seu deslocamento horizontal.

Determine o módulo e o sentido da força eletromotriz induzida no sistema como função do tempo , considerando os mesmos intervalos.

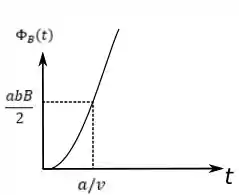
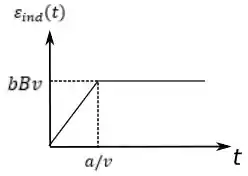
(c) Esboce os gráficos dos módulos do fluxo e da força eletromotriz induzida como função de , destacando os valores relevantes.

Vamos começar com item .

Temos que encontrar como a área varia com o tempo em cada intervalo de tempo.

No intervalo a barra se move no trecho em que os trilhos junto a barra formam um triangulo, já que é o tempo que ela leva para completar esse percurso.

A barra sempre se move na direção com uma velocidade então sua posição varia com o tempo, logo .

E enquanto ela está no trecho que os trilhos são inclinados o quanto que a barra está sobre esses trilhos vai aumentando com o tempo logo a posição na direção também varia com o tempo, logo temos um .

Então podemos estabelecer uma relação entre o triangulo de altura e base , com o triangulo formado pela barra es os trilhos, da seguinte forma:

Então no intervalo de tempo temos que é dado por:

Que é a área do triangulo, usando o que sabemos, temos:

E que , ficamos com:

No intervalo temos que a barra se encontra na parte retilínea do trilho.

Logo a área que ela forma com o trilho vai se dá pela soma da área do triangulo que não vai mais mudar com a de um retângulo que muda conforme a barra se move.

A área de um retângulo é dada pelo produto da base pela altura. Nesse caso a altura não muda ela tem o valor constante de .

Agora a base varia com o tempo, ela é dada pela posição menos que corresponde a parte do triângulo, logo temos que:

Usando que , temos:

Agora podemos encontrar o fluxo do campo para cada intervalo de tempo.

Primeiro para , temos:

Agora para , temos:

Prontinho o item está feito.

Vamos para o item .

Primeiro para o intervalo de tempo . Nesse intervalo temos:

Logo a força eletromotriz é dada por:

Agora para o intervalo , temos:

a força eletromotriz é dada por:

Item finalizado.

Agora vamos ver como fica os gráficos pedidos em .

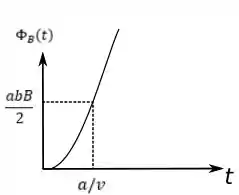
Primeiro para o módulo do fluxo que encontramos em .

No intervalo o fluxo tem o seguinte comportamento

E o no intervalo , temos:

Assim o gráfico fica da seguinte forma:

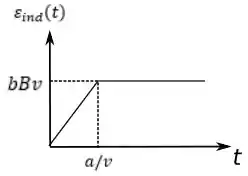
Agora o módulo da força eletromotriz que encontramos em .

No intervalo o fluxo tem o seguinte comportamento

E o no intervalo , temos:

Assim o gráfico fica da seguinte forma: