Um campo magnético uniforme, porém variável no tempo , induz uma força eletromotriz (fem) em uma espira de raio . Qual é a fem induzida na espira de raio ?
Passo 1
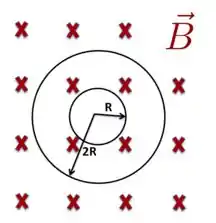
Neste problema, temos um campo magnético uniforme, ou seja, cujo valor é o mesmo em todos os pontos. Porém, esse valor não permanece o mesmo à medida que o tempo passa, ou seja, é um campo que é variável no tempo e suas linhas de campo entram no plano da página atravessando as áreas definidas pelas espiras. O valor dessas áreas permanecem os mesmos com o tempo e suas direções podem ser sempre tomadas como paralelas ao campo, como está ilustrado na figura abaixo por meio do vetor elemento de área .
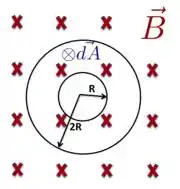
Por isso, a variação do fluxo magnético neste caso se dará por causa da taxa de variação do módulo .
Passo 2
Vamos calcular primeiro o fluxo magnético através da espira menor de raio . Para um determinado tempo arbitrário, o campo magnético é o mesmo em todos os pontos da área da espira e é paralelo à área da espira . Por isso, o fluxo magnético é dado por
Porém, lembre-se, estamos analisando este fluxo magnético está calculado para o um tempo fixo e arbitrário e, por essa razão, vale para todo tempo . Isso nos permite escrever
Para este caso, o módulo da fem induzida é
Essa é a fem induzida na espira menor. No entanto, o campo magnético variável também induz uma fem induzida na espira maior....
Passo 3
.... que, seguindo a mesma discussão anterior, e lembrando que área através da qual o campo magnético varia é maior e dada por , temos a seguinte fem induzida na espira maior
Resposta
Portanto, a resposta correta é dada na letra c).