Força e Torque sobre uma Espira, Lei de Faraday, Lei de Lenz
Um fio de massa , comprimento e resistência pode deslizar sem atrito, apoiado em dois trilhos horizontais, condutores e de resistência desprezível. Eles são ligados na extremidade esquerda por uma peça condutora, de modo que o conjunto todo forme uma espira condutora retangular.
Na região dos trilhos existe um campo magnético vertical uniforme e o fio de massa é puxado para a direita por uma força de módulo constante .
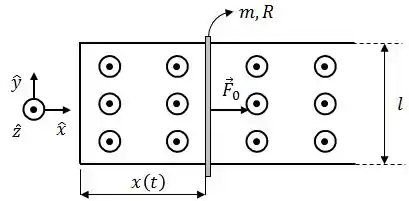
Calcule a e a corrente induzida no fio, indicando seus sentidos;
Calcule a força magnética que age sobre o fio, em função de sua velocidade;
Calcule a velocidade terminal (para ) do fio;
Quando o fio atinge essa velocidade, qual é a potência dissipada nele?
Passo 1
Calcule a e a corrente induzida no fio, indicando seus sentidos;
A induzida é calculada a partir da lei de Faraday, dada por:
Então precisamos calcular primeiro o fluxo magnético através da espira, que é dado por:
Como o campo magnético é constante, com módulo igual a , podemos reescrever o fluxo magnético como:
Onde , logo:
Substituindo na expressão de , teremos:
Sabendo que a velocidade do fio é dada por , podemos dizer que:
Assim, a é dada por:
Passo 2
A corrente induzida é dada por:
O sentido da corrente é determinado pela lei de Lenz, que diz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela diz é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
O fluxo magnético é dado por:
Logo:
Assim, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo, ou seja, o campo magnético induzido estará entrando no plano da página.
Para que o campo magnético induzido tenha esse sentido, a corrente induzida deve estar no sentido horário.
Passo 3
Calcule a força magnética que age sobre o fio, em função de sua velocidade;
A força magnética sobre um fio retilíneo é dada por:
Onde o vetor tem a mesma direção e sentido da corrente no fio, logo:
Substituindo esses caras na expressão de , teremos:
Assim, o módulo da força magnética será:
Passo 4
Calcule a velocidade terminal (para ) do fio;
O fio está sendo puxado para a direita por uma força e, devido à variação do fluxo magnético na espira, aparece uma força na direção oposta.
O fio alcançará a velocidade terminal quando
Assim, a força resultante sobre o fio será nula e ele permanecerá se movendo com velocidade constante.
Passo 5
Quando o fio atinge essa velocidade, qual é a potência dissipada nele?
A potência dissipada no fio será:
Substituindo a expressão de , teremos:
Onde nós acabamos de calcular:
Resposta
A corrente induzida está no sentido horário.