Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 121234567891011131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Coordenadas esféricas

Calcular a integral tripla

I = ∭ W   x 2 + y 2 + z 2   d x d y d z

Onde W é o sólido contido no primeiro octante entre as esferas x 2 + y 2 + z 2 = 4 e x 2 + y 2 + z 2 = 9 e acima do cone 3 z 2 = x 2 + y 2 .

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

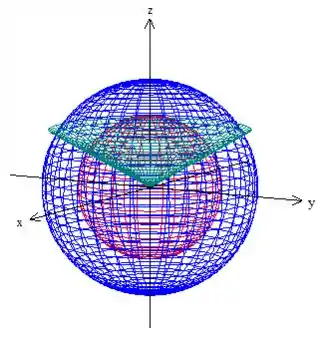
Temos duas esferas centradas na origem, com raios ρ = 2 e ρ = 3 e a folha superior de um cone (onde temos z ≥ 0 ).

Queremos a região do 1º octante compreendida entre essas duas esferas e acima do cone, como pede o enunciado, fazendo esses cortes, teremos então:

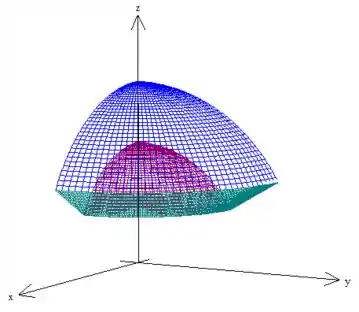
Passo 2

Como a região é limitada por duas esferas e um cone, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Passo 3

Precisamos agora escrever matematicamente a região de integração.

Pela própria figura, já vemos que 0 ≤ θ ≤ π / 2 (o que corresponde ao 1º octante). Os valores de ρ , nós vemos que variam desde a superfície da esfera menor até a da esfera maior. Traduzindo isso para coordenadas esféricas, temos 2 ≤ ρ ≤ 3 (pois as esferas estão centradas na origem!)

Falta, então, o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , onde temos φ = 0 até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:

3 ρ cos ⁡ φ = ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2

3 ρ cos ⁡ φ = ρ 2 s e n 2 φ cos 2 ⁡ θ + ( ρ 2 s e n 2 φ )   s e n 2 θ

3 ρ cos ⁡ φ = ρ 2 s e n 2 φ   = ρ   s e n   φ

s e n   φ = 3 cos ⁡ φ   → t g   φ = 3     →   φ = π / 3

Portanto, 0 ≤ φ ≤ π / 3 . A região será escrita como:

W = { ( ρ , θ , φ ) | 0 ≤ θ ≤ π / 2 ; 0 ≤ φ ≤ π / 3 ;   2 ≤ ρ ≤ 3 }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada. Sabemos que x 2 + y 2 + z 2 = ρ 2 (equação da esfera). Temos, então:

∫ 0 π / 3 ∫ 0 π / 2 ∫ 2 3 ρ 2 ρ 2 s e n   φ   d ρ   d θ   d φ =

= ∫ 0 π / 3 ∫ 0 π / 2 ∫ 2 3 ρ 3 s e n   φ   d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π / 3 ∫ 0 π / 2 ρ 4 4 s e n   φ ρ = 2 ρ = 3   d θ   d φ =

= ∫ 0 π / 3 ∫ 0 π / 2 65 4 s e n   φ   d θ   d φ =

Passo 6

Agora vamos integrar em relação a θ :

= 65 4 ∫ 0 π / 3 θ   s e n   φ θ = 0 θ = π / 2     d φ =

= 65 4 ∫ 0 π / 3 π 2   s e n   φ     d φ =

Passo 7

Finalmente, integrando em relação a φ :

= 65 π 8 - cos ⁡ φ 0 π / 3 =

= - 65 π 8 1 2 - 1 =

Resposta

65 π 16

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ