Calcule o volume do sólido que se encontra no interior da esfera de equação e acima da folha superior do cone de equação .
Passo 1
Bora lá, primeiro passo pra o sucesso é a gente conhecer a região que a gente está trabalhando.
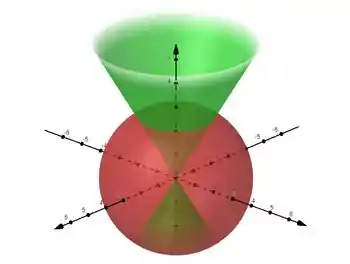
Nosso sólido entá dentro da esfera, e dentro da parte superior do cone, que está no eixo positivo.
Passo 2
Como a questão nos pede o volume, isso nada mais é do que
Passo 3
Pra resolver essa integral tripla, o método mais fácil é por coordenadas esféricas. Então:
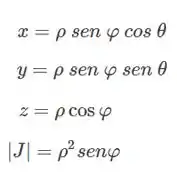
Passo 4
Então agora vamos colocar no papel nossos intervalos!
Uma vez que o da uma volta completa.
Passo 5
Montando a integral então, sem esquecer o :
Resposta
Exercícios de Livros Relacionados
Identifique a superfície com a equação dada. ρ cos ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen θ sen ϕ