Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 481234567891011121314151617181920212223242526272829303132333435363738394041424344454647495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Enunciado 3: Considere a região espacial

U = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ 9 ,   z ≥ 3 x 2 + 3 y 2 ,   x ≥ 0 ,   y ≥ 0

Calcule

I = ∭ U   y x 2 + y 2 + z 2   d x d y d z

Usando o método que preferir.

Passo 1

Primeiro vamos desenhar o nosso sólido para termos uma noção geométrica da coisa, ok?

x 2 + y 2 + z 2 ≤ 9

É uma esfera de raio 3 :

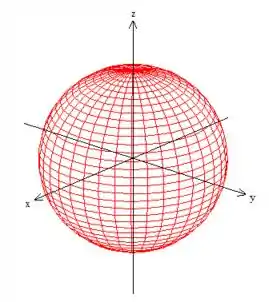
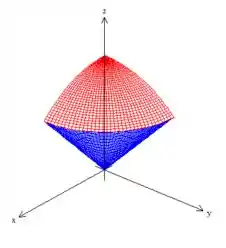
z ≥ 3 x 2 + 3 y 2 é um cone e esse sinal de maior significa apenas que estamos pegando a parte de dentro dele:

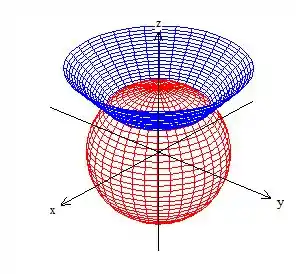
Como x ≥ 0 e y ≥ 0 , só queremos essa parte aqui do sorvete:

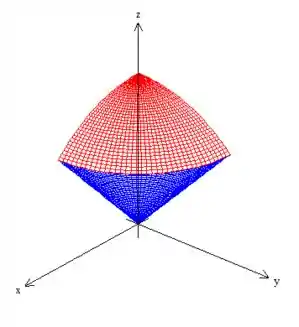
Passo 2

Podemos resolver utilizando as coordenadas esféricas:

x = ρ sin ⁡ ϕ cos ⁡ θ

y = ρ sin ⁡ ϕ sin ⁡ θ

z = ρ cos ⁡ ϕ

x 2 + y 2 + z 2 = ρ 2

J = ρ 2 sin ⁡ ϕ

Onde as coordenadas ariam dentro de uma esfera...

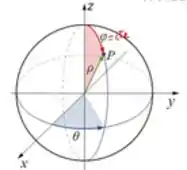
Passo 3

Para encontrar os limites dessa coordenadas aí no nosso sólido a gente deve comparar:

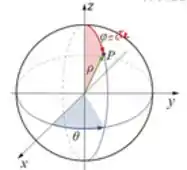
Veja que dessa vez o ρ varia de 0 até o raio da esfera máxima:

0 ≤ ρ ≤ 3

Enquanto isso, ângulo θ está variando de 0 até 90 ° que é quando atingimos a parede x = 0 :

0 ≤ θ ≤ π 2

Já o ângulo ϕ varia de 0   até o cone:

0 ≤ ϕ ≤ c o n e

Como o cone possui essa equação aqui:

z = 3 x 2 + 3 y 2     →

ρ cos ⁡ ϕ = 3 ρ 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ ϕ sin 2 ⁡ θ     →

ρ cos ⁡ ϕ = 3 ρ 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + sin 2 ⁡ θ     →

ρ cos ⁡ ϕ = 3 ρ 2 sin 2 ⁡ ϕ     →

ρ cos ⁡ ϕ = 3 ρ sin ⁡ ϕ   →

sin ⁡ ϕ cos ⁡ ϕ = 1 3   →     tan ⁡ ϕ = 3 3   →

ϕ = π 6

Então...

0 ≤ ϕ ≤ π 6

Passo 4

Remontando a integral...

I = ∭ U   y x 2 + y 2 + z 2   d x d y d z     →

I = ∫ 0 π 2 ∫ 0 π 6 ∫ 0 3 ρ sin ⁡ ϕ sin ⁡ θ ρ 2 ⋅ J   d ρ d ϕ d θ   →

Como J = ρ 2 sin ⁡ ϕ ...

I = ∫ 0 π 2 ∫ 0 π 6 ∫ 0 3 ρ sin 2 ⁡ ϕ sin ⁡ θ   d ρ d ϕ d θ =

∫ 0 π 2 ∫ 0 π 6 sin 2 ⁡ ϕ sin ⁡ θ ∫ 0 3 ρ   d ρ d ϕ d θ =

∫ 0 π 2 ∫ 0 π 6 sin 2 ⁡ ϕ sin ⁡ θ ρ 2 2 0 3 d ϕ d θ =

9 2 ∫ 0 π 2 sin ⁡ θ ∫ 0 π 6 sin 2 ⁡ ϕ d ϕ d θ

Fazendo a mudança...

sin 2 ⁡ ϕ = 1 - cos ⁡ 2 ϕ 2

9 2 ∫ 0 π 2 sin ⁡ θ ∫ 0 π 6 1 2 - cos ⁡ 2 ϕ 2 d ϕ d θ =

9 2 ∫ 0 π 2 sin ⁡ θ 1 2 ϕ - sin ⁡ 2 ϕ 4 0 π 6 d θ =

9 2 ∫ 0 π 2 sin ⁡ θ 1 2 ⋅ π 6 - sin ⁡ π 3 4 d θ =

9 2 π 12 - 3 8 ∫ 0 π 2 sin ⁡ θ d θ =

9 2 π 12 - 3 8 - cos ⁡ θ 0 π 2 =

9 2 π 12 - 3 8 - cos ⁡ π 2 - - cos ⁡ 0 =

9 2 π 12 - 3 8

Resposta

9 2 π 12 - 3 8

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ