Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 691234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2: Seja a > 0 uma constante. Seja

U = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ a 2 ,   z ≥ 0 .

Considere a integral tripla

J a = ∭ U   z 2 a 2 - x 2 - y 2 - z 2   d x d y d z

  1. Escreva J a numa forma de integral iterada, usando obrigatoriamente coordenadas esféricas.

    2. Obs.: Neste item não é necessário calcular a integral.

  2. Escreva J a numa forma de integral iterada, usando obrigatoriamente coordenadas cilíndricas.

    3. Obs.: Neste item não é necessário calcular a integral.

  3. Calcule J a .

Passo 1

a )

Como o próprio item nos pediu, devemos utilizar as mudanças para coordenadas esféricas, onde sempre realizamos a troca:

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

Onde as variáveis ρ , representa o raio e os ângulos φ e θ variam... Bem, aí é melhor te mostrar uma imagem:

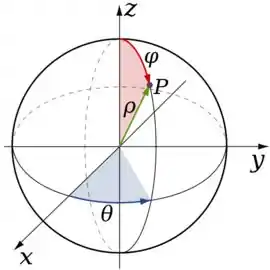
AHHH! Não podemos esquecer de que toda mudança nos exige uma correção pelo Jacobiano. No caso das esféricas, ele tem um formato bem manjado:

J = ρ 2 sin ⁡ φ

Uma equação que pode nos ajudar também é equação da esfera...

x 2 + y 2 + z 2 = ρ 2

Passo 2

Bem, nunca devemos terminar uma mudança sem antes determinar onde variam as coordenadas para a qual mudamos. No caso são elas: ρ , θ e φ .

Para determinar esses caras, é legal sabermos de uma forma geométrica com quem estamos lidando, ou seja, desenhar a região de integração U :

U = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ a 2 ,   z ≥ 0 .

Então, x 2 + y 2 + z 2 = a 2 nos representa uma esfera de raio a ... O sinal de menor ou igual só quer dizer que estamos dentro da esfera. Mas, esse ainda não é a região que queremos afinal o problema nos pede que tenhamos z ≥ 0 . Isso significa que precisamos cortar a esfera ao meio e pegar só a parte de cima:

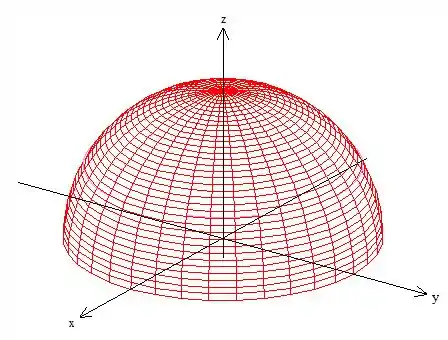
Passo 3

Bem, essa é a região de integração que estamos trabalhando. Se compararmos com as variações das coordenadas esféricas:

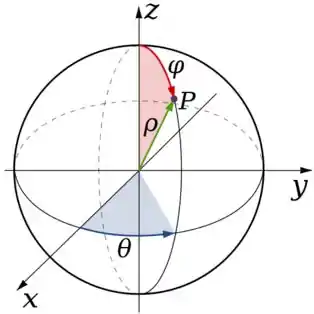
Dá para perceber que o raio ρ varia de 0 , a origem, até o raio máximo que delimita a região, no caso a ...

0 ≤ r ≤ a

No caso do ângulo θ , como esse ângulo gira ao redor do eixo z , e nossa superfície está dando uma volta completa nesse eixo, θ só pode estar girando de 0 ° até 360 ° ...

0 ≤ θ ≤ 2 π

Quanto ao outro ângulo φ , bem ele está saindo do 0 , e indo até o a metade da esfera, girando até 90 ° portanto...

0 ≤ φ ≤ π 2

Passo 4

Ok, agora só temos que ter mais um cuidado que é em mudar a função que estamos integrando...

z 2 a 2 - x 2 - y 2 - z 2

Temos que passar para as coordenadas esféricas...

z 2 a 2 - x 2 + y 2 + z 2 = ρ cos ⁡ φ 2 a 2 - ρ 2

Passo 5

Com essas variações...

0 ≤ r ≤ a

0 ≤ θ ≤ 2 π

0 ≤ φ ≤ π 2

Podemos reescrever a integral que queremos para a integral em coordenadas esféricas, apenas não se esqueça do Jacobiano...

J a = ∭ U   z 2 a 2 - x 2 - y 2 - z 2   d x d y d z =

∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ cos ⁡ φ 2 a 2 - ρ 2 ⋅ J d r d φ d θ

Como J = ρ 2 sin ⁡ φ ...

∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ cos ⁡ φ 2 a 2 - ρ 2 ⋅ ρ 2 sin ⁡ φ d r d φ d θ =

∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ 3 cos ⁡ φ sin ⁡ φ 2 a 2 - ρ 2 d r d φ d θ

Passo 6

b )

Agora vamos fazer a mesma coisa, mas dessa vez descrevendo a integral em coordenadas cilíndricas...

x = r cos ⁡ θ

y = r sin ⁡ θ

E o z não muda...

z = z

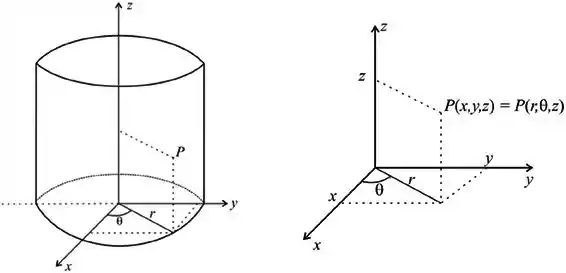
O Jacobiano dessa mudança é...

J = r

E uma equação que sempre é bom ter em mente quando se faz essa mudança é que...

x 2 + y 2 = r 2

Passo 7

Assim coo nas coordenadas esféricas, aqui também não saímos sem determinar as variações de no caso r , θ e z ...

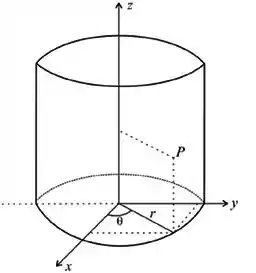
Por comparação, o θ aqui continua girando de

0 ≤ θ ≤ 2 π

Enquanto o r , agora se refere o raio do cilindro que contém o solido U . Como a o cilindro que contém o sólido precisa ter o mesmo raio que a semiesfera...

0 ≤ r ≤ a

Já o z , bem, para descobrir sua variação, vejamos que z varia do plano z = 0 até a esfera...

0 ≤ z ≤ E s f e r a

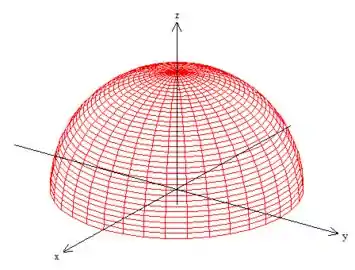
Como a esfera tem equação x 2 + y 2 + z 2 = a 2 , podemos isolar o z ...

x 2 + y 2 + z 2 = a 2     →               z 2 = a 2 - x 2 + y 2       →

z = a 2 - x 2 + y 2

Repare que pegamos apenas o lado positivo da raiz, pois queremos a parte de cima, saca?

0 ≤ z ≤ a 2 - x 2 + y 2               →

Em coordenadas cilíndricas...

0 ≤ z ≤ a 2 - r 2

Passo 8

Mudando a função que estamos integrando para as coordenadas cilíndricas...

z 2 a 2 - x 2 - y 2 - z 2 =

z 2 a 2 - x 2 + y 2 - z 2 =

z 2 a 2 - r 2 - z 2

Passo 9

Com essas variações

0 ≤ θ ≤ 2 π

0 ≤ r ≤ a

0 ≤ z ≤ a 2 - r 2

E a função em coordenadas cilíndricas e não se esquecendo do Jacobiano, montamos a integral

J a = ∭ U   z 2 a 2 - x 2 - y 2 - z 2   d x d y d z =

∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 z 2 a 2 - r 2 - z 2 ⋅ J   d z d r d θ =

∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 r z 2 a 2 - r 2 - z 2   d z d r d θ

Passo 10

Pegando a integral em coordenadas cilíndricas, pois parece mais fácil de calcular a integral...

∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 r z 2 a 2 - r 2 - z 2   d z d r d θ

E calculando a integral de dentro em z ...

∫ 0 2 π ∫ 0 a r ∫ 0 a 2 - r 2 z 2 a 2 - r 2 - z 2   d z d r d θ

Precisamos realizar uma mudança...

2 a 2 - r 2 - z 2 = u     →

d u = - 2 z d z         o u           z d z = - d u 2

Não esqueça de mudar também os limites da variável...

z = 0                 →               u = 2 a 2 - r 2 - 0 2 = 2 a 2 - r 2

z = a 2 - r 2                 →               u = 2 a 2 - r 2 - a 2 - r 2 2 = a 2

Substituindo na integral...

∫ 0 2 π ∫ 0 a r - ∫ 2 a 2 - r 2 a 2 1 u   d u 2 d r d θ =

∫ 0 2 π ∫ 0 a r - u 2 a 2 - r 2 a 2 d r d θ =

∫ 0 2 π ∫ 0 a r - a 2 - 2 a 2 - r 2 d r d θ = ∫ 0 2 π ∫ 0 a r 2 a 2 - r 2 - r a   d r d θ =

∫ 0 2 π ∫ 0 a r 2 a 2 - r 2   d r d θ - ∫ 0 2 π ∫ 0 a r a   d r d θ

Calculando a primeira integral...

Passo 11

∫ 0 2 π ∫ 0 a r 2 a 2 - r 2   d r d θ

Fazendo outra mudança do ripo...

2 a 2 - r 2 = v       →           d v = - 2 r d r           o u           r d r = - d v 2

r = 0                     →                       v = 2 a 2 - 0 2 = 2 a 2

r = a                     →                       v = 2 a 2 - a 2 = a 2

e substituindo na integral...

∫ 0 2 π ∫ 0 a r 2 a 2 - r 2   d r d θ = 1 2 ∫ 0 2 π ∫ 2 a 2 a 2 v   - d v d θ =

1 2 ∫ 0 2 π ∫ a 2 2 a 2 v   d v d θ = 1 2 ∫ 0 2 π 2 3 v v a 2 2 a 2 d θ =

1 2 ∫ 0 2 π 2 3 2 a 2 2 a 2 - 2 3 a 2 a 2 d θ =

Como a é um número...

1 2 4 2 3 a 3 - 2 3 a 3 ∫ 0 2 π d θ = 1 2 4 2 3 a 3 - 2 3 a 3 2 π =

4 2 π 3 a 3 - 2 π 3 a 3

Passo 12

Calculando então a outra integral...

∫ 0 2 π ∫ 0 a r a   d r d θ = a ∫ 0 2 π ∫ 0 a r   d r d θ =

a ∫ 0 2 π r 2 2 0 a d θ = a ∫ 0 2 π a 2 2 d θ =

a 3 2 2 π = π a 3

Passo 13

Juntando todas as duas integrais que calculamos separadas...

∫ 0 2 π ∫ 0 a r 2 a 2 - r 2   d r d θ - ∫ 0 2 π ∫ 0 a r a   d r d θ =

4 2 π 3 a 3 - 2 π 3 a 3 - π a 3 =

4 2 π 3 a 3 - 5 π 3 a 3

Resposta

a )     ∫ 0 2 π ∫ 0 π 2 ∫ 0 a ρ 3 cos ⁡ φ sin ⁡ φ 2 a 2 - ρ 2 d r d φ d θ

b )     ∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 r z 2 a 2 - r 2 - z 2   d z d r d θ

c )       4 2 π 3 a 3 - 5 π 3 a 3

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ