Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 261234567891011121314151617181920212223242527282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja I = ∭ D z x 2 + y 2 d V ,   onde D é o sólido entre os cones z = - x 2 + y 2 3 e z = - 3 x 2 + y 2 e as esferas x 2 + y 2 + z 2 = 4 e x 2 + y 2 + z 2 = 9 .

  • Descreva o sólido D em coordenadas esféricas ρ ,   ϕ ,   θ .
  • Calcule I .

Passo 1

1º ponto) Antes de descrever o sólido em coordenadas polares, vamos entende-lo um pouquinho melhor?

Bem, pra entender os cones, vamos desenhar as projeções deles no plano Z X zerando Y

  1. Primeiro cone

    2. z = - x 2 + y 2 3     ⇒     z = - x 2 3

    Extraindo a raiz, lembrando do fato que x 2 = x

    z = - 1 3 x

  2. O segundo cone, de forma parecida, teremos

z = - 3 x 2 + y 2       ⇒     z = - 3 x 2

z = - 3   | x |

Observe que a primeira curva é aquela função módulo pra baixo pois é negativo e mais aberto que a segunda devido o coeficiente angular - 1 3 é em módulo menor que o módulo de - 3 .

Veja só!

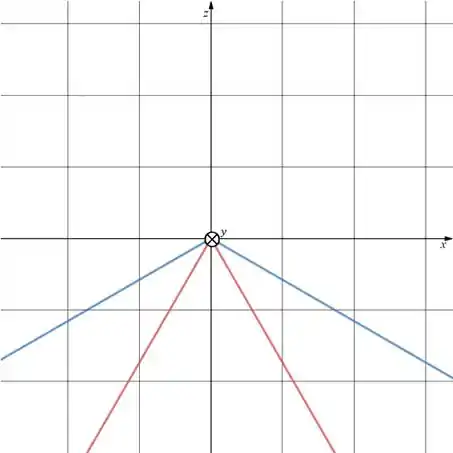
Em azul está essa função mais aberta, a primeira função, enquanto que a segunda está em vermelha, viu?!

girando esses módulos em torno de z , vamos ganhar os cones:

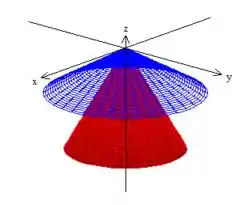
Agora delimitando o sólido pelas esferas, vamos obter

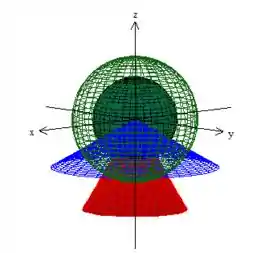
Passo 2

Bem... pra descrever esse sólido em coordenadas esféricas, a gente vai usar

x = ρ sin ⁡ ϕ cos ⁡ θ

y = ρ sin ⁡ ϕ sin ⁡ θ

z = ρ cos ⁡ ϕ

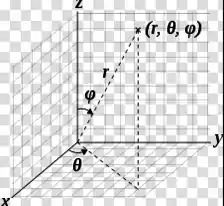
Observe que ρ está variando da esfera menor de raio 2, até a maior de raio 3, ou seja

2 ≤ ρ ≤ 3

Esse θ , como temos um giro completo em torno de z , teremos

0 ≤ θ ≤ 2 π

Passo 3

Quanto a esse ângulo ϕ , o que está limitando eles são nossos cones! Em um deles temos:

z = - x 2 + y 2 3

ρ cos ⁡ ϕ = - ρ 2 sin 2 ⁡ ϕ 3

ρ cos ⁡ ϕ = - ρ sin ⁡ ϕ 3

cos ⁡ ϕ = - sin ⁡ ϕ 3

tan ⁡ ϕ = - 3

Lembra que tan ⁡ 60 ° = 3 ? Então o ângulo cuja tangente é - 3 é justamente o ϕ = - 60 ° = - π 3 !

Achamos um limite pra ϕ , falta o outro:

z = - 3 x 2 + y 2

ρ cos ⁡ ϕ = - 3 ρ 2 sin 2 ⁡ ϕ

ρ cos ⁡ ϕ = - ρ sin ⁡ ϕ 3

cos ⁡ ϕ = - sin ⁡ ϕ 3

tan ⁡ ϕ = - 1 3

Agora lembra que tan ⁡ 30 ° = 1 3 ? Então o ângulo cuja tangente é - 1 3 é ϕ = - 30 ° = - π 6 !

Então encontramos os limites de ϕ ! Só que não haha. Se liga que nós encontramos eles usando o plano x y como origem, mas devíamos ter usado o eixo z ! Simplificando isso que eu acabei de falar, a gente achou os ângulos pretos, mas precisamos dos ângulos verdes:

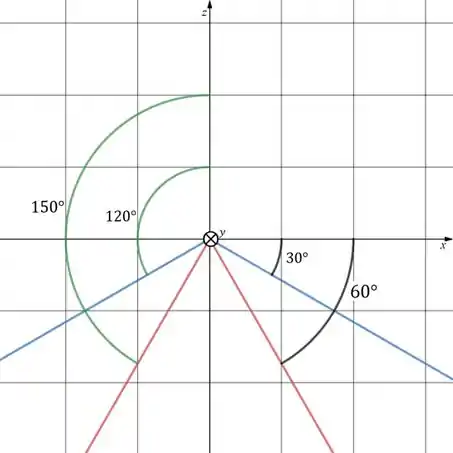
Foi? Temos que:

120 ° = 2 π 3

150 ° = 5 π 6

Então:

2 π 3 ≤ ϕ ≤ 5 π 6

Passo 4

2º ponto) Bora resolver a integral com as nossas novas coordenadas?:)

I = ∭ D z x 2 + y 2 d V =

AHHH! E não se esqueça do jacobiano que deve ser encaixado nas mudanças

J = ρ 2 sin ⁡ ϕ

∭ D ρ , ϕ ,   θ ρ cos ⁡ ϕ   ρ sin ⁡ ϕ cos ⁡ θ 2 + ρ sin ⁡ ϕ sin ⁡ θ 2 ∙ J d V

Substituindo os limites encontrados no primeiro ponto e simplificando tudo

∫ 0 2 π ∫ 2 3 ∫ 2 π 3 5 π 6 ρ cos ⁡ ϕ ∙ ρ 2 sin ⁡ ϕ ρ 2 sin 2 ⁡ ϕ ( sin 2 ⁡ θ + cos 2 ⁡ θ ) d ϕ d ρ d θ =

∫ 0 2 π ∫ 2 3 ∫ 2 π 3 5 π 6 ρ cos ⁡ ϕ sin ⁡ ϕ d ϕ d ρ d θ

Prontinho! Integral montada, agora é só correr pro abraço!:)

Pois bem... vamos resolver a integral de dentro por uma substituição

sin ⁡ ϕ = u ⇒       d u = cos ⁡ ϕ d ϕ

Não se esqueça de mudar os limites também

ϕ = 5 π 6 →     u = sin ⁡ 5 π 6 = 1 2

ϕ = 2 π 3 → u = sin ⁡ 2 π 3 = 3 2

∫ 0 2 π ∫ 2 3 ∫ 2 π 3 5 π 6 ρ cos ⁡ ϕ sin ⁡ ϕ d ϕ d ρ d θ = ∫ 0 2 π ∫ 2 3 ∫ 3 2 1 2 ρ d u u d ρ d θ

∫ 0 2 π ∫ 2 3 ρ ln ⁡ u 3 2 1 2 d ρ d θ

∫ 0 2 π ∫ 2 3 ρ ln ⁡ 1 2 - ln ⁡ 3 2 d ρ d θ

Tirando essa constante multiplicativa e integrando o polinômio em ρ e depois em θ

I = ln ⁡ 1 2 - ln ⁡ 3 2 ∫ 0 2 π ∫ 2 3 ρ d ρ d θ

I = ln ⁡ 1 2 - ln ⁡ 3 2 ∫ 0 2 π ρ 2 2 2 3 d θ

I = ln ⁡ 1 2 - ln ⁡ 3 2 ∫ 0 2 π 9 2 - 4 2 d θ

I = 2 π 5 2 ln ⁡ 1 2 - ln ⁡ 3 2

Cortando esse 2 e lembrando que ln ⁡ 1 2 - ln ⁡ 3 2 = ln ⁡ 1 2 3 2 = ln ⁡ 1 3

I = 5 π ln ⁡ 1 3

Resposta

1º ponto:

x = ρ sin ⁡ ϕ cos ⁡ θ

y = ρ sin ⁡ ϕ sin ⁡ θ

z = ρ cos ⁡ ϕ

Onde

2 ≤ ρ ≤ 3

0 ≤ θ ≤ 2 π

2 π 3 ≤ ϕ ≤ 5 π 6

2º ponto:

I = 5 π ln ⁡ 1 / 3

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ