Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

(7) A descrição do cilindro x 2 + y 2 = 1 , entre os planos z = 0 e z = 1 , em coordenadas esféricas ρ ,   θ ,   ϕ , é dada por:

  1. ρ sin ⁡ ϕ = 1 ,               π / 4 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π
  2. ρ sin ⁡ ϕ = 1 ,           -   π / 2 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π
  3. ρ sin ⁡ ϕ ≤ 1 ,               π / 4 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π
  4. ρ sin ⁡ ϕ = 1 ,               0 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π
  5. ρ sin ⁡ ϕ ≤ 1 ,               0 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π

Passo 1

Bem, o cilindro que queremos descrever é essa casquinha aqui, oh:

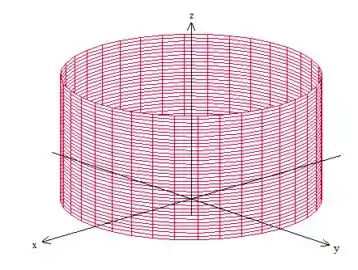
Se queremos descreve-lo em coordenadas esféricas, é bem válido vermos que mudança é essa certo? E ela é esta daqui, oh:

x = ρ sin ⁡ ϕ cos ⁡ θ

y = ρ sin ⁡ ϕ sin ⁡ θ

z = ρ cos ⁡ ϕ

Bem, descrever o cilindro nada mais é do que encontrar a variação de ρ , ϕ e θ que formam o cilindro.

Passo 2

Comecemos com o ρ , aqui. :D

Para encontra-lo, basta substituir as equações da mudança na equação do cilindro que onde ele realmente está, saca?

x 2 + y 2 = 1       →

ρ sin ⁡ ϕ cos ⁡ θ 2 + ρ sin ⁡ ϕ sin ⁡ θ 2 = 1   →

ρ 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ ϕ sin 2 ⁡ θ = 1   →

Colocando em evidência...

ρ 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + sin 2 ⁡ θ = 1   →

E lembrando que cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

ρ 2 sin 2 ⁡ ϕ = 1   →

ρ sin ⁡ ϕ = 1

(usualmente isolaríamos o ρ , mas a resposta esta escrita assim, então, neh!...)

Passo 3

Quanto ao ângulo ϕ , bem esse ângulo sempre varia saindo do eixo z , por isso é valido fazermos a projeção dessa superfície no plano Y Z :

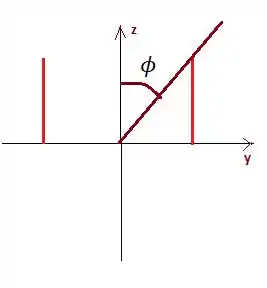
Note que o ϕ está começando lá na extremidade superior do cilindro e descendo até completar 90 ° :

S u p e r i o r ≤ ϕ ≤ π 2

Essa extremidade tem z = 1 ...

z = ρ cos ⁡ ϕ       →           ρ cos ⁡ ϕ = 1

Já vimos que o ρ = 1 sin ⁡ ϕ ...

    1 sin ⁡ ϕ cos ⁡ ϕ = 1    

Invertendo essas frações:

sin ⁡ ϕ cos ⁡ ϕ = 1       →         tan ⁡ ϕ = 1

Logo ϕ = 45 ° ...

π 4 ≤ ϕ ≤ π 2

Passo 4

Como todas as opções mostram θ

  0 ≤ θ ≤ 2 π

Ele só pode ser esse cara, mas só para que você saiba, ele é de 0 até 2 π , pois ele varia nessa mudança no plano X Y :

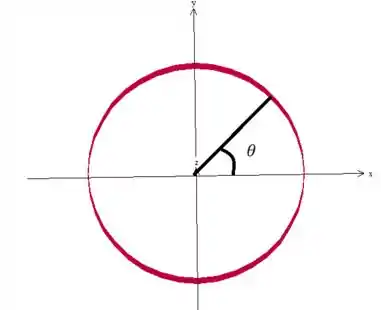
Como o cilindro ao redor de z da uma volta completa, θ só pode girar uma volta completa, saca?

Resposta

a )     ρ sin ⁡ ϕ = 1 ,               π / 4 ≤ ϕ ≤ π / 2 ,                   0 ≤ θ ≤ 2 π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ