Calcule
onde é o sólido formado pelos pontos que estão acima do cone dentro da esfera e fora da esfera
Passo 1
Só de ler esse enunciado, vendo todas esses , logo pensamos nas coordenadas esféricas, não?
Lembra como é a substituição pra coordenadas esféricas? Chamamos
Sem esquecer ainda o jacobiano

Passo 2
Substituindo esses valores no nosso cone teremos
Logo
Passo 3
Tranquilo!! Para analisarmos a variação de só prestarmos atenção na região onde estamos trabalhando. Temos que o raio vai variar entra a circunferência maior e menor, ou seja, entre e fora da esfera
Caso você não tenha visto isso logo de cara, pode substituir os valores das coordenadas esféricas nessas funções e vai achar o que estou te falando
Fazendo o mesmo para outra equação
Quanto a variação de é só lembrando que estamos dando uma voltinha completa, sem restrições.
Passo 4
Agora é só montarmos nossa integral. Uma coisa que preciso que você se lembre é como os angulos variam
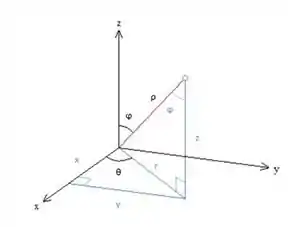
Observe que a região que queremos está ACIMA de que é um cone virado para cima.
Como é o eixo z, teremos que nossa região terá variando entre zero e . Caso quisessemos a região ABAIXO do cone, teriamos entre o variando entre e , tranquilo? Agora sim vamos então montar e resolver nossa integral.