Calcule
Onde é a esfera
Passo 1
Oi, tudo bem?
O problema nos pediu para calcularmos essa integral tripla:
Onde os limites de integração são essa esfera aqui

Como temos uma integral tripla e a região de interesse é uma esfera, então é interessante usarmos coordenadas esféricas! Então a ideia aqui é transformar todo esse integrando em coordenadas esféricas, assim como a região dos limites de integração.
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos dar uma olhada com mais carinho na nossa integral tripla:
Vamos trocar primeiro o diferencial. Em retangulares é esse aí que vemos
Mas em esféricas fica assim:
Beleza?
E o integrando? O integrando fica assim:
Que lembra uma equação de esfera! Por isso a facilidade de integrar em esféricas essa coisa!
Nossa integral ficou assim:
Beleza até aqui!

Passo 3
Agora vamos arrumar os limites de integração!
A região é dentro da esfera de raio 3 centrada na origem:
Então o raio vai de até :
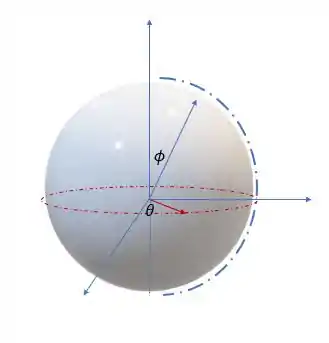
Como queremos a região total da esfera o varia de até (da porção positiva do eixo até a negativa) e de até . Assim nossa integral com os limites fica assim:
Tudo bem até aqui?

Vamos calcular essa integral? Bora lá!
Passo 4
Como não temos função/limite de integração, nada que dependa de , então podemos transferir o para a última integral (a mais de fora) e já resolver. Podemos também resolver a mais interna (que depende de ), tudo junto. Aí temos o seguinte
Agora é só aplicar nos limites:
Tranquilo até aqui?

Passo 5
Agora vamos calcular a última integral em :
Ufa! Agora sim! Terminamos! Espero ter ajudado!
Até próxima!