Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 421234567891011121314151617181920212223242526272829303132333435363738394041434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 4: Seja E a região sólida interna à esfera x 2 + y 2 + z 2 = 6 , limitada por cima pelo cone

z = x 2 + y 2 2

E por baixo pelo plano x y .

  1. Expresse a integral que representa o volume de E em coordenadas esféricas.
  2. Expresse a integral que representa o volume de E em coordenadas cilíndricas.
  3. Calcule o volume de E usando o resultado de um dos itens anteriores.

Passo 1

Bem, antes de passarmos para a resolução das letras propriamente dito, é muito válido desenharmos a região primeiro, já que vamos utiliza-la muito aqui nos itens, certo?

Como o próprio problema nos disse, se trata de uma superfície no interior de uma esfera, mas que está abaixo de um cone e acima do plano x y , então...

Eis o nosso volume ;)!

Passo 2

a )

Para descrever o sólido em coordenadas esféricas devemos trocar então...

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

Não podemos nos esquecer do jacobiano dessa mudança que é

J = ρ 2 sin ⁡ φ

E nem de que a equação da esfera em coordenadas esféricas é:

x 2 + y 2 + z 2 = ρ 2

Passo 3

Show, mas necessitamos de determinar a variação desses termos ( ρ , φ e θ ):

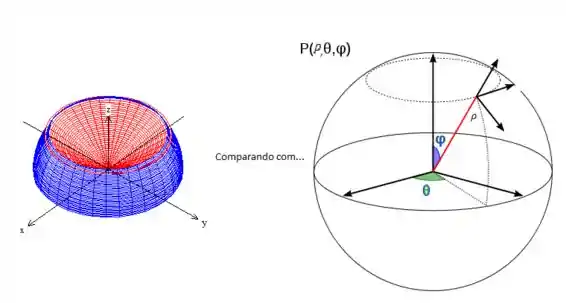
Comparando a variação desses caras no espaço com a nossa região, vemos que...

0 ≤ ρ ≤ r a i o   d a   e s f e r a     →

0 ≤ ρ ≤ 6

Enquanto θ , tem que dar uma volta completa...

0 ≤ θ ≤ 2 π

Já o φ , bem, esse vai dar um pouquinho de mais trabalho, já que φ entra no sólido pelo cone e vai até 90 ° ...

c o n e ≤ φ ≤ π 2

Como o cone tem equação z = x 2 + y 2 2 , basta trocar as coordenadas esféricas aí ver onde a gente chega...

z = x 2 + y 2 2       →               �� cos ⁡ φ = ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ φ sin 2 ⁡ θ 2     →

  ρ cos ⁡ φ = ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ 2           →               ρ cos ⁡ φ = ρ 2 sin 2 ⁡ φ 2         →

Como sin ⁡ φ   é maior que 0 , então...

ρ cos ⁡ φ = ρ sin ⁡ φ   2         →             2 = ρ sin ⁡ φ   ρ cos ⁡ φ         →

tan ⁡ φ = 2

Logo, a gente vê que o φ sai do arco cuja tangente é 2 ( arctan ⁡ 2 ) até 90 ° ...

arctan ⁡ 2 ≤ φ ≤ π 2

Passo 4

Montando a integral lembrando que a integral que calcula volume é...

V o l = ∭ S   1   d V

Onde o S , a gente vai trocar pelas variações e, além disso, vamos multiplicar o 1 pelo Jacobiano...

V o l = ∫ 0 2 π ∫ arctan ⁡ 2 π 2 ∫ 0 6 ρ 2 sin ⁡ φ   d ρ d φ d θ

Passo 5

b )

Beleza, vamos descrever a integral, mas agora nas coordenas cilíndricas, onde devemos substituir...

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

O jacobiano agora é

J = r

E

x 2 + y 2 = r 2

Passo 6

Novamente, vamos determinar a variação dos termos que são agora r , θ e z .

Quero que você veja que podemos tomar o sólido como um conjunto de váaaaarios “anéis” de raio diferente definido pela intersecção de um plano paralelo ao x y com o sólido:

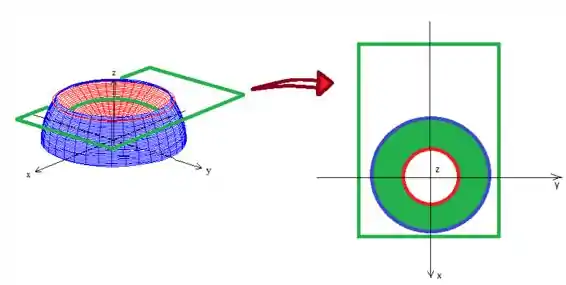
Visualizar o sólido dessa forma é legal, pois a gente percebe que o r sempre varia do cone até o raio maior que é o da esfera.

C o n e   v e r m e l h o ≤ r ≤ E s f e r a   a z u l

Como a equação do cone é

z = x 2 + y 2 2           →             z = r 2 2         →

r = 2 z

E o da esfera é...

x 2 + y 2 + z 2 = 6         →           r 2 = 6 - z 2         →

r = 6 - z 2

Veja então que assim ganhamos a variação de r ...

2 z ≤ r ≤ 6 - z 2

Observando o anel, θ , continua dando uma volta completa...

0 ≤ θ ≤ 2 π

Enquanto que o z , varia de 0 , até o limite máximo de z que se dá na intersecção das suas

0 ≤ z ≤ i n t e r s e c ç ã o

Como a equação das duas são em coordenas cilindricas...

r = 2 z r = 6 - z 2

6 - z 2 = 2 z         →             6 - z 2 = 2 z 2         →               z 2 = 2           →

z = 2

Onde concluímos que o z varia de 0 até 2 ...

0 ≤ z ≤ 2

Passo 7

Então o volume em coordenadas cilíndricas é...

V o l = ∭ S   1 d V =

∫ 0 2 π ∫ 0 2 ∫ 2 z 6 - z 2 J d r d z d θ =

∫ 0 2 π ∫ 0 2 ∫ 2 z 6 - z 2 r d r d z d θ

Passo 8

c )

Para calcular o volume podemos utilizar qualquer uma das duas integrais que montamos. Vamos pegar a segunda que é mais fácil por não envolver seno e tal...

∫ 0 2 π ∫ 0 2 ∫ 2 z 6 - z 2 r d r d z d θ = ∫ 0 2 π ∫ 0 2 ∫ 2 z 6 - z 2 r d r d z d θ =

Calculando essa integral de dentro primeiro em r ...

∫ 0 2 π ∫ 0 2 r 2 2 2 z 6 - z 2 d z d θ = ∫ 0 2 π ∫ 0 2 6 - z 2 2 2 - 2 z 2 2 d z d θ =

Substituindo os limites e depois calculando a integral dupla que surgir, vamos ganhar...

∫ 0 2 π ∫ 0 2 6 - z 2 2 - 2 z 2 2 d z d θ = ∫ 0 2 π ∫ 0 2 3 - 3 2 z 2   d z d θ =

∫ 0 2 π 3 z - z 3 2 0 2 d θ = ∫ 0 2 π 3 2 - 2 3 2 d θ =

3 2 - 2 2 2 2 π =

4 2 π

Resposta

a )       V o l = ∫ 0 2 π ∫ arctan ⁡ 2 π 2 ∫ 0 6 ρ 2 sin ⁡ φ   d ρ d φ d θ

b )     ∫ 0 2 π ∫ 0 2 ∫ 2 z 6 - z 2 r d r d z d θ

c )     4 2 π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ