Calcule onde
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos um elipsoide “deformado” em e um cone, também “deformado” na mesma direção:
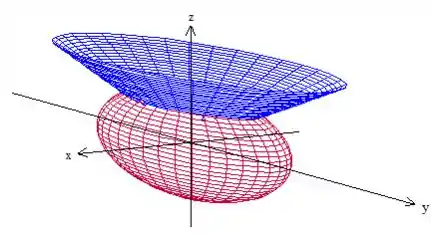
A região do problema é aquela que está dentro do elipsoide e abaixo do cone contida no primeiro octante.
Passo 2
Como a região é limitada por um elipsoide, vamos utilizar coordenadas esféricas com os coeficientes do elipsoide:
Passo 3
Precisamos escrever matematicamente a região de integração. Como “transformamos” o elipsoide em uma esfera de raio com essa mudança de coordenadas, podemos dizer que:
Você pode verificar isso fazendo a mudança esférica na sua equação!
O ângulo , como vemos pela figura, varia desde a superfície do cone até (lembre-se de que a região está no primeiro diedro. Então, vamos fazer a mudança esférica no cone:
Já que temos de volta em torno do eixo , (lembra que nossa região se limita ao primeiro diedro). Isso nos dá:
Passo 4
Vamos agora fazer a substituição esférica na integral:
Passo 5
Agora vamos integrar em relação a :
Passo 6
Agora em relação a :