Seja a região sólida corresponde à calota esférica acima do plano e abaixo da esfera . Escreva a integral correspondente ao volume da região :
a) Utilizando coordenadas cilíndricas.
b) Utilizando coordenadas esféricas.
c) Escolha uma das integrais dos itens a) ou b) e resolva para encontrar o volume da região .
Passo 1
a) Cara, ele diz que temos uma região que está acima de e abaixo da esfera . E nos pede o volume.
Para achar esse volume a gente pode montar uma integral tripla.
E como ele pede, vamos começar usando as coordenadas cilíndricas.
Para usar coordenadas cilíndricas para descrever essa região, a gente precisa fazer a mudança de variáveis:
E limitar e . Aí como a gente faz isso? Primeiro vamos olhar para o eixo . Nele a gente diz entre quais superfícies nossa região está.
Se a nossa região está abaixo da esfera e acima de , ela está em . Podemos dizer, então, que ela está abaixo da parte de cima da nossa esfera, que tem essa equação:
E acima do plano . E aí podemos dizer que está limitado dessa forma:
Passo 2
Limitar e é como percorrer a região do plano onde a região está contida, só que em coordenadas polares.
Para gente, essa região vai ser a parte do plano que está dentro da projeção da interseção entre a esfera e o plano . Vamos achar a equação dessa interseção:
Temos então, a região dentro da circunferência de raio 1.
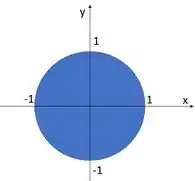
Como é um círculo completo, a gente diz que:
E como é o segmento que sai da origem e vai até a borda do círculo:
Ufa! Vamos seguir.
Passo 3
Agora é escrever a integral. A tem que colocar os extremos de integração, aplicar a mudança de variáveis no integrando e multiplicar o integrando por . Aí fazendo essas coisinhas, ficamos com:
Só falta aplicar a mudança de variáveis nos extremos de integração
Prontinho!
Passo 4
b) Vamos fazer agora com as coordenadas esféricas. Precisamos fazer a mudança:
Como a gente está abaixo da parte de cima da esfera, podemos dizer que estamos do lado de dentro da esfera, assim:
Substituindo as expressões das coordenadas:
E como a gente está acima do plano , podemos dizer que
Substituindo nossas expressões
Aí o fica assim:
é o mesmo ângulo das coordenadas cilíndricas, então ele vai ter esse intervalo:
Passo 5
Falta limitar . Como a gente faz isso? Cara, podemos usar as informações do item anterior. A gente viu que a projeção da nossa região é um círculo de raio . E ela está limitada pelo plano está na altura .
A gente tem então, tipo uma calota de carro na altura . Se a gente olhar uma vista lateral da nossa região, temos algo assim:
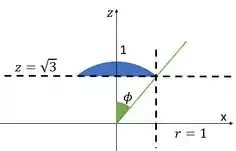
Temos que é o ângulo que sai do eixo e vai até a reta que sai da origem e passa pelo ponto . É o ângulo verdinho.
Aí para achar ele, a gente pode usar identidades trigonométricas.
Aí nosso fica:
Passo 6
Agora é escrever a integral. Aí tem que colocar os extremos de integração, aplicar a mudança de variáveis e multiplicar o integrando por . Aí fazendo essas coisinhas, ficamos com:
Prontinho!
Passo 7
c) Chegamos no grande momento. Que integral usar? A mais fácil! E qual é? A que tem o integrando e os extremos de integração mais simples.
Comparando as duas, vemos que uma tem extremos com funções trigonométricas no denominador. Isso é já é uma dica de que a primeira é melhor.
Percebe que o integrando da primeira é só o . Então ele também é mais simples. Vamos então de coordenadas cilíndricas! Calculando essa belezura:
Vamos usar a substituição simples nessa que tem a raiz:
Uhul! Arrasamos!
Resposta
a)
b)
c)