Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 721234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a integral tripla

∭ Ω   x 2 + y 2 z 2   d V ,

Onde Ω = x ,   y ,   z   |     x 2 + y 2 + z 2 ≤ z .

Passo 1

Bem, antes de calcular essa integral aí, vamos fazer entender a região de integração: bem, se essa equação é uma equação de uma esfera, mas não é uma esfera comum com o centro na origem, como estamos acostumados, pois ela está deslocada da origem:

x 2 + y 2 + z 2 ≤ z         →             x 2 + y 2 + z 2 - z ≤ 0           →

Lembrando que z - 1 2 2 = z 2 - z + 1 4 ...

x 2 + y 2 + z - 1 2 2 - 1 4 ≤ 0     →

x 2 + y 2 + z - 1 2 2 ≤ 1 4

Perceba que é uma esfera de raio 1 / 2 deslocado de meia unidade em z ...

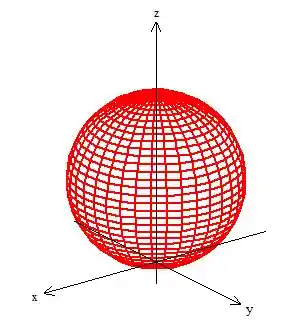
Passo 2

Se estamos querendo uma integral tripla em uma esfera, nada mais justo que trabalharmos com as coordenadas esféricas...

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

E o Jacobiano é...

J = ρ 2 sin ⁡ φ

SHOW! Agora vamos encontrar onde essas novas variáveis variam dentro do nosso sólido ;)

Passo 3

Para encontrar essa variação, uma sugestão é sempre comparar o desenho do nosso sólido com o a variação das variáveis esféricas:

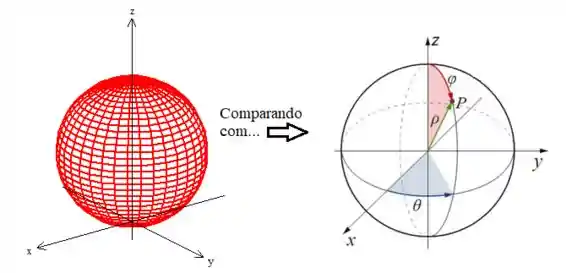
Veja que o ângulo θ tem que dar uma volta completa para formar a esfera deslocada:

0 ≤ θ ≤ 2 π

Enquanto o ângulo φ , ele está saindo de 0 ° e indo até 90 ° , saca?

0 ≤ φ ≤ π 2

Já o raio ρ , bem, esse está variando da origem e indo até a esfera deslocada...

0 ≤ ρ ≤ E s f e r a   d e s l o c a d a

Como vimos no enunciado, essa esfera tem equação x 2 + y 2 + z 2 = z . Substituindo então pelas coordenadas esféricas...

x 2 + y 2 + z 2 = z               →  

ρ sin ⁡ φ cos ⁡ θ 2 + ρ sin ⁡ φ sin ⁡ θ 2 + ρ cos ⁡ φ 2 = ρ cos ⁡ φ     →

ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ φ sin 2 ⁡ θ + ρ 2 cos 2 ⁡ φ = ρ cos ⁡ φ   →

ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ + ρ 2 cos 2 ⁡ φ = ρ cos ⁡ φ   →

ρ 2 sin 2 ⁡ φ + ρ 2 cos 2 ⁡ φ = ρ cos ⁡ φ   →

ρ 2 sin 2 ⁡ φ + cos 2 ⁡ φ = ρ cos ⁡ φ   →

ρ 2 = ρ cos ⁡ φ   →

ρ = cos ⁡ φ

Logo...

0 ≤ ρ ≤ E s f e r a   d e s l o c a d a       →

0 ≤ ρ ≤ cos ⁡ φ

Passo 4

Agora é só voltar para a integral mesmo... (Não se esqueça do Jacobiano):

∭ Ω   x 2 + y 2 z 2   d V = ∫ 0 2 π ∫ 0 π 2 ∫ 0 cos ⁡ φ ρ sin ⁡ φ cos ⁡ θ 2 + ρ sin ⁡ φ sin ⁡ θ 2 ρ cos ⁡ φ 2 ⋅ J   d ρ d φ d θ =

∫ 0 2 π ∫ 0 π 2 ∫ 0 cos ⁡ φ ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + ρ 2 sin 2 ⁡ φ sin 2 ⁡ θ ρ cos ⁡ φ 2 ⋅ ρ 2 sin ⁡ φ   d ρ d φ d θ =

∫ 0 2 π ∫ 0 π 2 ∫ 0 cos ⁡ φ ρ 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ ρ 2 cos 2 ⁡ φ ⋅ ρ 2 sin ⁡ φ   d ρ d φ d θ =

∫ 0 2 π ∫ 0 π 2 ∫ 0 cos ⁡ φ ρ 2 sin 3 ⁡ φ cos 2 ⁡ φ   d ρ d φ d θ

Integrando em relação a ρ ...

∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos 2 ⁡ φ ∫ 0 cos ⁡ φ ρ 2   d ρ d φ d θ = ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos 2 ⁡ φ ρ 3 3 0 cos ⁡ φ d φ d θ =

∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos 2 ⁡ φ ⋅ cos 3 ⁡ φ 3 d φ d θ = 1 3 ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos ⁡ φ d φ d θ =

Integrando agora com relação a φ ...

1 3 ∫ 0 2 π sin 4 ⁡ φ 4 0 π 2 d θ = 1 3 ∫ 0 2 π sin 4 ⁡ π 2 4 - sin 4 ⁡ 0 4 d θ =

1 3 ∫ 0 2 π 1 4 d θ = 1 12 ∫ 0 2 π d θ =

1 12 2 π = π 6

Resposta

π 6

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ