Integrais Triplas, Coordenadas Esféricas
Considere a região espacial definida por
Calcule
Passo 1
Primeiro, vamos dar uma analisada na região que estamos integrando? Esse deve ser sempre o primeiro passo, vai ajudar muito a visualizar!
A primeira desigualdade diz que está entre e . Bom, sabemos que é a equação de uma esfera de raio né? Então, essa região se trata do volume entre as esferas centradas na origem de raio e !
A segunda desigualdade diz que , ou seja, tomando esse volume entre as duas esferas, estamos apenas na parte superior, com positivo ;)
Juntando essas duas informações em uma imagem, é a região entre as calotas vermelha e verde:
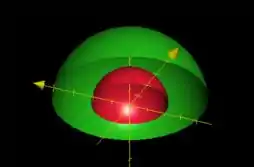
Passo 2
Agora, podemos ir na fé com coordenadas esféricas! Chamando:
Show! E a região , como ela fica? Colocando as novas coordenadas, teremos:
Tirando a raiz dos dois lados na primeira desigualdade, teremos:
Pelo desenho, vemos que varia entre e , enquanto varia entre e , show?
Passo 3
Colocando os limites e o novo sistema de coordenadas, e, claro, sem esquecer do jacobiano, a integral fica:
Cortando os , fica:
Integrando em relação a , teremos:
Show!
Passo 4
Agora, vamos integrar em relação a . Para isso, temos que lembrar que . Colocando essa relação a integral, temos:
E podemos integrar tranquilamente , o que dá:
E, agora, podemos integrar em relação a , que dá:
Resposta
A integral dá