UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P1 2022.1, Questão 5
Seja a parte da região limitada pela superfície , externa à . Esboce o perfil da região e calcule
Passo 1
Oiie, tudo bem com você?
Temos aqui uma região descrita em coordenadas esféricas como a região entre as superfícies
e
precisamos usar essa região para calcular
além de esboçar a região! Para começar, vamos tentar visualizar a nossa região e então determinar limites de integração que permitam a resolução de nosso problema! Bora lá!
Passo 2
A superfície é como se fosse uma rosquinha da forma
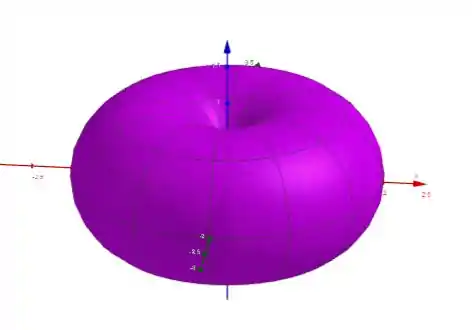
e, a função é um cilindro da forma
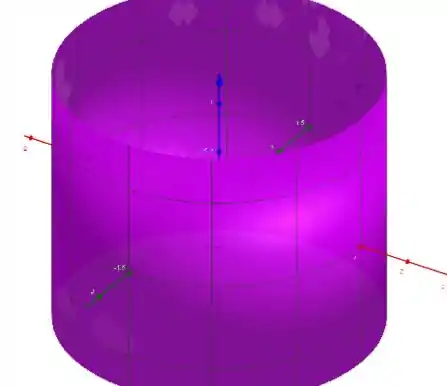
Note que o cilindro radialmente é interno à rosquinha, portanto, nossa integração será feita a partir do cilindro até a superfície exterior. No entanto, temos a vantagem de a rosquinha ter simetria esférica, portanto, a integral poderá ser calculada em coordenadas esféricas! Saca só!
Passo 3
Se usarmos que
, e
obtemos que , usando também o elemento de volume esférico como , em que , e , temos que resolver a seguinte integração
É necessário fazer a integral em primeiro, mas esta é bastante direta, temos que
De forma que nos resta resolver
Vamos resolver as integrais que faltam! Saca só!
Passo 4
TEmos que resolver a seguinte integral
note que , por isso simplificamos o segundo integrando acima. Vamos resolver a integral mais complicada primeiro. Usando que temos que
Aqui temos simplesmente que
e, também que
De forma que
Nos restando as seguintes integrais
note que já substituí a integral em no segundo termo, já que mostrei o resultado dela enquanto resolvia a integral anterior, belezinha? Bora só escrever o nosso resultado final agora!
Passo 5
A integral que resta é identificada como
Portanto, temos que a nossa integral se torna
A questão foi isso! Te vejo na próxima! Tchau Tchau!