Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 511234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule ∫ - 2 0 ∫ 0 4 - x 2 ∫ - 4 - x 2 - y 2 0 x 2 y z   d z d y d x via coordenadas esféricas.

Passo 1

Pois bem, a primeira coisa que a gente tem que ter em mente para resolver esse exercício é a sólido. Então vamos começar com uma pergunta: quem é esse sólido?

Pra responder essa pergunta, vamos começar tirando da integral definida os intervalos de variação de x , y e z

0 ≤ x ≤ - 2

0 ≤ y ≤ 4 - x 2

EPA!!! Espera aí um momento! Apareceu uma configuração bem típica. Uma região do tipo 1, pois x está variando em um intervalo numérico bem definido e y entre funções, se lembra?! :D

Mas ainda está um pouco complicado de ver que região é essa, não está? Vamos fazer o seguinte, vamos passar essa raiz aí para o outro lado

y 2 ≤ 4 - x 2

Jogando esse x também pro lado esquerdo...

y 2 + x 2 ≤ 4

Veja! É um círculo de raio dois! Mas queremos apenas a parte onde x é negativo e y positivo, ou seja

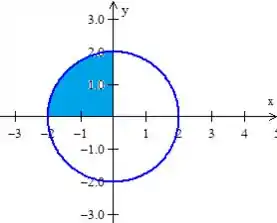
Pois bem, ainda nos falta ver onde z está variando:

- 4 - x 2 - y 2 ≤ z ≤ 0

Preste a atenção na igualdade   - 4 - x 2 - y 2 = z . Podemos utilizar o mesmo artifício acima e tirar essa raiz daí

z 2 = 4 - x 2 - y 2

z 2 + x 2 + y 2 = 4

Olha que interessante, chegamos em uma esfera! Mas queremos apenas a parte de baixo dela, pois z ≤ 0 .

Juntando essa informação com a informação da variação de x e y e formos para o espaço...

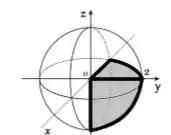
Passo 2

Note que é perfeito aplicar coordenadas esféricas aí!

x = ρ sen ⁡ φ cos ⁡ θ

y = ρ sen ⁡ φ   sen ⁡ θ

z = ρ cos ⁡ φ  

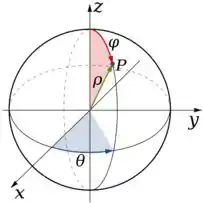
Onde o Jacobiano vale

J = ρ 2 sen ⁡ φ  

Perfeito! Agora a gente tem que procurar a variação dessas novas variáveis. Vem comigo!

Passo 3

Veja que θ varia no plano X Y no sentido anti-horário positivo, logo, ele entrará no nosso sólido em 90 ° e vai até 180 ° . Ou seja

π 2 ≤ θ ≤ π

Quanto ao ângulo φ   , podemos perceber que ele desce no sentido positivo, então ele também entrará no sólido em π 2 e sairá em π .

π 2 ≤ φ ≤ π

Por fim, o raio ρ varia da origem até o limite de raio da esfera que é 2 . :)

0 ≤ r ≤ 2

Passo 4

Prontinho! Agora é só correr para o abraço e resolver essa integral aí! :D

∫ - 2 0 ∫ 0 4 - x 2 ∫ - 4 - x 2 - y 2 0 x 2 y z   d z d y d x =

Trocando essas variáveis aí pelas novas coordenadas... ah! Cuidado para não esquecer do produto pelo jacobiano!

∫ π 2 π ∫ π 2 π ∫ 0 2 ρ sen ⁡ φ cos ⁡ θ 2 .   ρ sen ⁡ φ   sen ⁡ θ   .   ρ cos ⁡ φ   .   J   d ρ d φ d θ =  

∫ π 2 π ∫ π 2 π ∫ 0 2 ρ 2 sen 2 ⁡ φ cos 2 ⁡ θ   . ρ sen ⁡ φ   sen ⁡ θ   .   ρ cos ⁡ φ   .   ρ 2 sen ⁡ φ   d ρ d φ d θ =

Simplificando mais um pouquinho...

∫ π 2 π ∫ π 2 π ∫ 0 2 ρ 6 sen 4 ⁡ φ cos 2 ⁡ θ sen ⁡ θ   cos ⁡ φ d ρ d φ d θ =

Resolvendo primeiro a integral de dentro em relação a ρ , obteremos

∫ π 2 π ∫ π 2 π cos 2 ⁡ θ sen ⁡ θ sen 4 ⁡ φ cos ⁡ φ   ρ 7 7 0 2 d φ d θ =

128 7 ∫ π 2 π ∫ π 2 π cos 2 ⁡ θ sen ⁡ θ sen 4 ⁡ φ cos ⁡ φ   d φ d θ =

Considerando θ constante agora e integrando em relação a φ fazendo uma substituição do tipo sen ⁡ φ = u , logo d u = cos ⁡ φ   d φ , não esquecendo de mudar os limites

φ = π 2       ⇒       u = sen ⁡ π 2 = 1

φ = π       ⇒       u = sen ⁡ π = 0

Teremos

128 7 ∫ π 2 π ∫ 1 0 cos 2 ⁡ θ sen ⁡ θ u 4   d u d θ =

128 7 ∫ π 2 π cos 2 ⁡ θ sen ⁡ θ u 5 5 1 0 d θ =

Substituindo os limites e tirando a constante para fora, ficaremos

128 7   .   - 1 5 ∫ π 2 π cos 2 ⁡ θ sen ⁡ θ d θ =

Por fim, resolvendo essa integral aí de modo análogo, fazendo uma substituição do tipo

v = cos ⁡ θ       ⇒         d v = - sen ⁡ θ d θ

Mudando também os limites de integração

θ = π 2         ⇒           v = cos ⁡ π 2 = 0

θ = π         ⇒       cos ⁡ π = - 1

Cuidado com o sinal! Vamos passar esse sinal negativo de - 1 5 para próximo do sen ⁡ θ dentro da integral

128 7   .   - 1 5 ∫ π 2 π cos 2 ⁡ θ sen ⁡ θ d θ = 128 35 ∫ π 2 π cos 2 ⁡ θ ( - sen ⁡ θ d θ ) =

128 3 5 ∫ 0 - 1 v 2 d v

Resolvendo essa última integral aí

128 3 5 v 3 3 0 - 1 = 128 25 - 1 3 3 =

- 128 105

Resposta

∫ π 2 π ∫ π 2 π ∫ 0 2 ρ 6 sen 4 ⁡ φ cos 2 ⁡ θ sen ⁡ θ   cos ⁡ φ d ρ d φ d θ = - 128 105

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ