UFSC, Joinvile, Cálculo II, Provas Profº Rómulo Castillo - P2 2015.1, Questão 5c
Dadas o conjunto , formule
uma integral que calcule o volume do sólido T:
c) usando integrais triplas em coordenadas esféricas. (Neste caso, resolva somente a pri-
meira integral interna)
Passo 1
Eaew, belezinha?
O enunciado da questão pede para a gente escrever uma integral para calcular o volume da região T, definida por duas inequações. Primeiro, vamos olhar a primeira parte da primeira inequação:
A gente reconhece que, quando vale a igualdade, essa expressão descreve uma esfera centrada na origem do sistema de coordenadas. No caso da inequação, estamos interessados nos pontos contidos na superfície da esfera e os pontos nas superfícies de outras esferas, com raio menor ou igual à 2, como descrito pela inequação
Então, a nossa região T, está contida entre duas esferas de raio 1 e de raio 2. No entanto, há uma terceira expressão, cuja igualdade descreve um cone:
No caso da inequação, estamos interessados nos pontos acima da superfície cônica, mas que estejam contidos entre as esferas de raio 1 e 2. A figura a seguir ilustra a região T contida entre a esfera de raio 1, a esfera de raio 2 e o cone, respectivamente em verde, vermelho e azul.
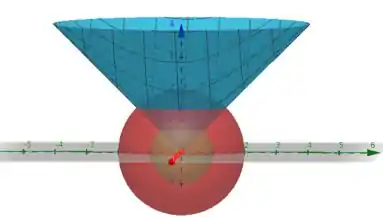
Para descrever o volume de uma região através de uma integral, tudo o que precisamos fazer é somar os volumes infinitesimais dV dentro dos limites da região T
Então, só precisamos escrever o elemento de volume em coordenadas esféricas e descobrir quais são os limites de integração para as variáveis que descrevem a região T. Então vamos lá!
Passo 2
Em coordenadas esféricas, um infinitésimo de volume pode ser escrito em termo de variações infinitesimais das coordenadas como:
Então, o volume da região T é dado pela integral
Agora, só precisamos descobrir os limites de integração da região T!
Passo 3
Como a região está contida entre duas esferas de raio 1 e raio 2, temos que a coordenada r está restrita conforme:
Quanto ao ângulo azimutal , temos que a região contém todos os valores possíveis da coordenada, visto que a região completa “uma volta inteira” em torno do eixo z. Então, os limites de integração de são
Agora, para o ângulo polar , temos que a nossa região está contida entre um cone, que possui inclinação em relação ao plano xy de 45 graus. Portanto, como o ângulo é medido a partir do eixo z, temos que a coordenada , na região T, varia desde 0 rad até rad. Então:
Agora já podemos escrever a integral do volume com os limites apropriados de interação!
Resolvendo a integral interna (em r), obtemos