Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 191234567891011121314151617182021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

  1. Calcule ∭ W z   d V , onde W é o sólido limitado pelas superfícies z = x 2 + y 2 , z = 3 x 2 + y 2 e x 2 + y 2 + z 2 = 4 .

Passo 1

Pow! Para começar exercícios como esse, sim, vamos começar como sempre é recomendado: desenhando o sólido W ;)

Bem, esse sólido é formado por dois cones centrados na origem: z = x 2 + y 2 e z = 3 x 2 + y 2

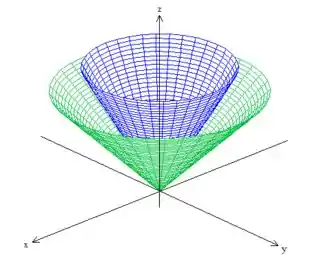
só que está delimitado na lateral por essa esfera de raio 2 , x 2 + y 2 + z 2 = 4 , nos dando o sólido W .

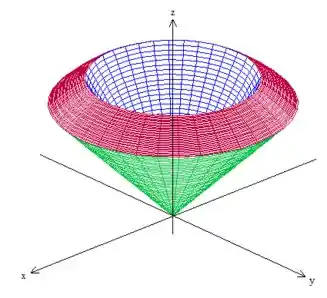
Passo 2

Bem, como estamos trabalhando dentro de uma esfera, nada mais legal que pensarmos em uma mudança para coordenadas esféricas

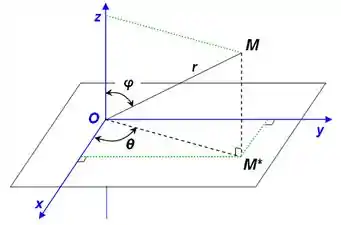
onde vamos trocar

x = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

z = r cos ⁡ φ                  

O jacobiano dessa mudança é

J = r 2 sin ⁡ φ

Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?

Passo 3

Vamos começar aqui falando do mais fácil, o raio! Bem, ele está variando da origem até o raio limite que é o da própria esfera:

0 ≤ r ≤ R a i o   d a   e s f e r a

0 ≤ r ≤ 2

Esse ângulo θ também é bem fácil, basta você observar que a esfera dá uma volta completa ao redor do eixo z , logo

0 ≤ θ ≤ 2 π

Quanto ao ângulo φ , bem... Ele é um pouquinho mais chato, mas não se preocupe que você vai pegar fácil também, vêm comigo separado

Passo 4

Bem, se você reparar novamente no sólido,

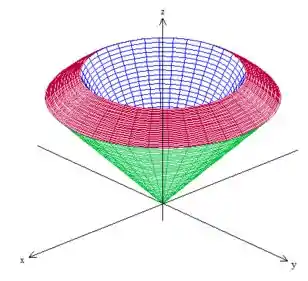
você vai notar que o ângulo φ está variando de um cone até o outro:

C o n e   v e r d e ≤ φ ≤ C o n e   a z u l

Ambos têm equação bem parecida: z = x 2 + y 2 e z = 3 x 2 + y 2 . Epa! Estamos trabalhando com as coordenadas polares, então devemos substitui-las nessas equações, veja em relação ao primeiro, z = x 2 + y 2

z = x 2 + y 2                   →                           r cos ⁡ φ = r sin ⁡ φ cos ⁡ θ 2 + r sin ⁡ φ sin ⁡ θ 2                     →

      r cos ⁡ φ = r 2 sin 2 ⁡ φ cos 2 ⁡ θ + r 2 sin 2 ⁡ φ sin 2 ⁡ θ     ��                   →

    r cos ⁡ φ = r 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ = r 2 sin 2 ⁡ φ

Como o seno é positivo e o raio também...

r cos ⁡ φ = r sin ⁡ φ     →         1 ∙   r cos ⁡ φ = r sin ⁡ φ

passando esse r cos  ⁡ φ pro outro lado dividindo...

r sin ⁡ φ r cos ⁡ φ = 1           →           tan ⁡ φ = 1

Nessas condições, φ = 45 ° = π 4

Fazendo a mesma análise com o outro cone z = 3 x 2 + y 2 ...

r cos ⁡ φ = 3   r 2 sin 2 ⁡ φ   →

1 ∙   r cos ⁡ φ = 3     r sin ⁡ φ   →  

r sin ⁡ φ r cos ⁡ φ = 1 3     →             tan ⁡ φ = 1 3

Logo φ = 30 ° = π 6

Logo

π 6 ≤ φ ≤ π 4

Passo 5

Bem, agora é só montar a integral tripla e correr para o abraço!

∭ W   z   d V

Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo J a c o b i a n o ;)

∫ 0 2 π ∫ π 6 π 4 ∫ 0 2 r cos ⁡ φ   J   d r d φ d θ =

∫ 0 2 π ∫ π 6 π 4 ∫ 0 2 r cos ⁡ φ   r 2 sin ⁡ φ   d r d φ d θ = ∫ 0 2 π ∫ π 6 π 4 ∫ 0 2   r 3 sin ⁡ φ cos ⁡ φ   d r d φ d θ

Integrando o de dentro e substituindo os limites de integração

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos ⁡ φ ∫ 0 2   r 3   d r d φ d θ =

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos ⁡ φ r 4 4 0 2 d φ d θ =

4 ∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos ⁡ φ d φ d θ =

Realizando uma mudança simples, integramos a do meio

sin ⁡ φ = t       →           d t = cos ⁡ φ d φ

(troque também os limites de integração)

φ = π 6           →               t = sin ⁡ π 6 = 1 2

φ = π 6           →               t = sin ⁡ π 4 = 2 2

Retornando a integral, substituindo e calculando, concluímos que

4 ∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos ⁡ φ d φ d θ = 4 ∫ 0 2 π ∫ 1 2 2 2 t   d t d θ =

4 ∫ 0 2 π ∫ 1 2 2 2 t   d t d θ =

4 ∫ 0 2 π t 2 2 1 2 2 2 d θ =

1 2 ∫ 0 2 π d θ = π

Resposta

π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ