Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 551234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Coordenadas Cilíndricas, Coordenadas Esféricas

Seja U a região do espaço definida por

U = { ( x , y , z ) ∈ R 3 | z 2 ≥ x 2 + y 2 ,   x 2 + y 2 + z 2 ≤ 2 ,   z ≥ 0 }

Considere a função

f x , y , z = z 2 x 2 + y 2 + z 2 1 / 3

E a integral tripla

I = ∭ U   f ( x , y , z ) d x d y d z

a) Escreva I na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas ( r , θ , z ) . (Neste item não é pedido o cálculo da integral.)

b) Escreva I na forma de uma integral iterada, usando obrigatoriamente coordenadas esféricas ( ρ , φ , θ ) . (Neste item não é pedido o cálculo da integral.)

c) Calcule I .

Passo 1

Resolvendo a letra a) da questão:

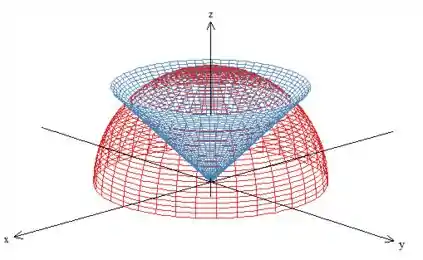
Vamos, antes de tudo, fazer um esboço para entender melhor a questão. Temos a parte positiva de uma esfera de raio r = 2 e a parte positiva de um cone com eixo de simetria z , o que nos dá uma semiesfera e um semicone. Queremos, então, a região compreendida entre essas duas superfícies.

Passo 2

Para descrever a região em coordenadas cilíndricas, faremos a seguinte substituição nas equações das superfícies:

x = r cos ⁡ θ

y = r   s e n   θ

z = z

Para o semicone:

z 2 = x 2 + y 2   → z 2 = r 2 cos 2 ⁡ θ + r 2 s e n 2 θ   → z = r

Para a semiesfera:

x 2 + y 2 + z 2 = 2   → r 2 cos 2 ⁡ θ + r 2 s e n 2 θ + z 2 = 2   → z = 2 - r 2  

(Queremos apenas as partes com z ≥ 0 )

Pela figura, vemos que os valores de z variam entre o semicone e a semiesfera, temos r ≤ z ≤ 2 - r 2 . Vemos, também, que 0 ≤ θ ≤ 2 π , uma vez que o sólido está envolta do eixo de simetria z .

Falta, então, o intervalo de r . Veja que essa coordenada varia desde r = 0 (o eixo z ) até onde as duas superfícies se cortam, então, vamos fazer a interseção entre suas equações:

z = r = 2 - r 2

r 2 = 2 - r 2

2 r 2 = 2

r = 1

Temos, então, 0 ≤ r ≤ 1 , o que nos dá:

U = { ( r , θ , z ) | 0 ≤ r ≤ 1 ,   0 ≤ θ ≤ 2 π ,   r ≤ z ≤ 2 - r 2 }

Passo 3

Agora vamos escrever a função f ( x , y , z ) em coordenadas cilíndricas:

z 2 x 2 + y 2 + z 2 1 / 3   → z 2 r 2 cos 2 ⁡ θ + r 2 s e n 2 θ + z 2 1 / 3 = z 2 r 2 + z 2 1 / 3    

Passo 4

Reescrevendo a integral em coordenadas cilíndricas, temos, então:

∫ 0 1 ∫ 0 2 π ∫ r 2 - r 2 z 2 r 2 + z 2 1 / 3     r   d z d θ d r

Não se esqueça do fator de conversão r .

Passo 5

Resolvendo a letra b) da questão:

Para descrever a região em coordenadas esféricas, faremos a seguinte substituição nas equações das superfícies:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

Para o semicone ( z ≥ 0 )

z = x 2 + y 2

ρ cos ⁡ φ = ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2  

ρ cos ⁡ φ = ρ 2   s e n 2   φ    

ρ cos ⁡ φ = ρ   s e n φ

t g   φ = 1   →   φ = π / 4

Para a semiesfera ( z ≥ 0 )

x 2 + y 2 + z 2 = 2   →   ρ = 2

Agora vamos escrever os intervalos. Pela própria figura, já vemos que 0 ≤ θ ≤ 2 π , uma vez que o sólido está envolta do eixo de simetria z . Os valores de φ devem variar entre o eixo z , onde φ = 0 e a superfície do cone, onde φ = π / 4 . A coordenada ρ varia desde ρ = 0 (na origem) até a superfície da esfera, onde ρ = 2 . Temos, então:

U = ρ , φ , θ |   0 ≤ θ ≤ 2 π ,   0 ≤ φ ≤ π / 4 ,   0 ≤ ρ ≤ 2

Passo 6

Agora vamos escrever a função f x , y , z = z 2 x 2 + y 2 + z 2 1 3 em coordenadas esféricas:

ρ cos ⁡ φ 2 ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 1 / 3 =  

= ρ cos ⁡ φ 2 ρ 2 / 3 =

= ρ 8 / 3 cos 2 ⁡ φ

Passo 7

Reescrevendo a integral em coordenadas esféricas, temos:

∫ 0 2 π ∫ 0 π / 4 ∫ 0 2 ρ 8 / 3 cos 2 ⁡ φ ρ 2 s e n   φ   d ρ d φ d θ   = ∫ 0 2 π ∫ 0 π / 4 ∫ 0 2 ρ 14 / 3 cos 2 ⁡ φ s e n   φ   d ρ d φ d θ  

Não se esqueça do fator de conversão, o Jacobiano J = ρ 2 s e n   φ

Passo 8

Resolvendo a letra c) da questão:

= ∫ 0 2 π ∫ 0 π / 4 3 ρ 17 / 3 17 cos 2 ⁡ φ s e n   φ   d φ d θ ρ = 0 ρ = 2 =

= 3 × 2 17 / 6 17 ∫ 0 2 π ∫ 0 π / 4 cos 2 ⁡ φ s e n   φ   d φ d θ =

= 3 × 2 17 / 6 17 ∫ 0 2 π - cos 3 ⁡ φ 3 φ = 0 φ = π / 4   d θ =

= 2 17 / 6 17 ∫ 0 2 π - 2 3 / 2 8 - 1   d θ =

= 4 × 2 5 / 6 17 ∫ 0 2 π 8 - 2 3 / 2 8   d θ =

= 2 5 / 6 ( 8 - 2 3 / 2 ) 2 × 17 θ θ = 0 θ = 2 π   d θ =

=   2 5 / 6 ( 8 - 2 3 / 2 ) π 17 =

Resposta

( 8 2 5 6 - 4 2 3 ) π 17

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ