Seja a região formada pelos pontos tal que
a)Esboce
b)Calcule o volume de usando a integral tripla.
Passo 1
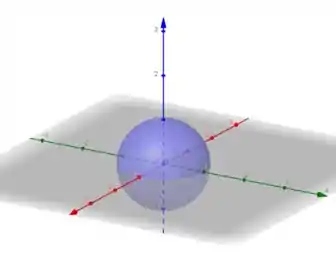
Vamos começar esboçando a inequação que é a região de dentro de uma esfera de raio .
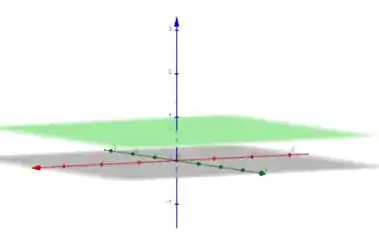
Agora temos que é a região acima do plano mostrada na imagem a seguir
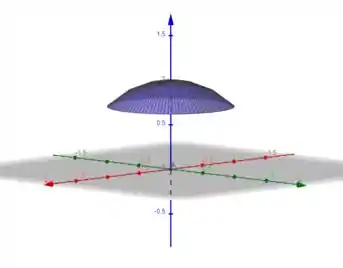
Como nossa região está acima desse plano e dentro da circunferência, o que temos é uma calota esférica
Passo 2
Letra b)
Como a questão nos pede o volume da região por uma integral tripla o que precisamos fazer é
Usando uma função constante igual a 1, o resultado é o produto das integrais dos infinitesimais ,e , o que corresponde nesse caso o volume do meu domínio que é a região.
Passo 3
Calcular nessas coordenadas é bem trabalhoso então o mais indicado é realizarmos uma mudança de variável. Mas qual mudança usar??
Eu poderia tanto fazer a mudança para coordenadas esféricas quanto para coordenada cilíndricas mas nessa questão vou usar a cilíndrica.
Passo 4
Precisamos encontrar os limites de integração após a mudança de variável
Para
Nosso vai variar de até a esfera. Isolando o na equação
Como nosso só está variando para valores positivos podemos esquecer aquele sinal de menos ali. Então nosso vai variar de:
Substituindo e :
Colocando r em evidência e lembrando da relação trigonométrica fundamental
Para :
Da intersecção da esfera com o plano temos:
Substituindo e :
Colocando em evidência:
Usando que
Mas como só admite valores positivos porque se trata do raio
Para finalizar, para teta, nossos limites serão e . Isso porque toda vez que seccionarmos teremos um circulo completo
Passo 5
Agora podemos resolver nossa integral tripla com a mudança de variável
Onde é o nosso domínio após a mudança de variável
Integrando com relação a :
Integrando com relação a :
Vamos primeiro separar em duas integrais
Resolvendo a primeira por uma substituição simples:
Vou multiplicar por para poder aparecer um e assim conseguir substituir por
Realizando a substituição:
Integrando com relação a
Colocando em evidência:
Resolvendo para teta:
Resolvendo a outra integral:
Resolvendo para teta:
Vamos ter então:
Manipulando um pouco vamos ter:
Passo 6
Resposta
a)
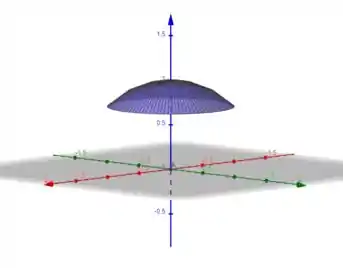
b)