Calcule o valor da integral
Onde .
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Completando o quadrado da expressão da superfície, temos:
Uma esfera de raio centrada em , portanto, deslocada no eixo .
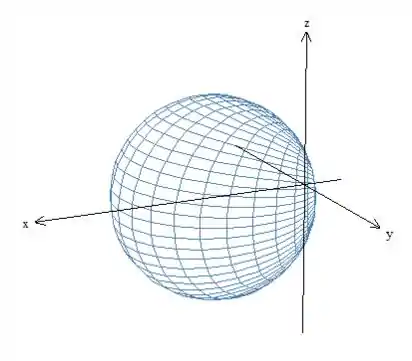
Passo 2
Essa região de integração parece simples, não é? Sim, mas, quando fazemos a mudança para coordenadas esféricas , como temos feito até agora, a integral se torna uma expressão não muito agradável, envolvendo e . Vamos, então, tentar contornar esse problema.
Uma esfera centrada na origem é escrita em coordenadas polares como , como já vimos. Essa esfera do problema, por estar deslocada, seria escrita como . Mas porque temos agora essa expressão bem mais complicada? Porque agora, não temos mais a simetria em relação à origem, pois a distância dos pontos da esfera ao ponto não é mais constante.
Temos, então, duas saídas para tornar a região de integração mais simétrica em relação aos eixos coordenados.
Solução 1: Essa solução é a mais abrangente. Se você reparar, as coordenadas esféricas são definidas com uma certa simetria em relação ao eixo . Como assim? O ângulo é medido em torno desse eixo e o ângulo , a partir desse eixo. Por isso, quando temos uma esfera deslocada em , sua equação não fica tão complicada como quando está deslocada nos outros eixos.
Partindo dessa ideia, podemos, então, fazer uma mudança esférica diferente, atribuindo não ao eixo , mas ao eixo de simetria da região, no caso, o eixo . Teremos, então:
Dessa forma a esfera seria escrita como . Essa solução seria muito útil se tivéssemos uma região mais complexa com simetria em .
Os limites nesse caso seriam:
Se quiser resolver assim pode tentar, mas a gente vai fazer aqui da forma 2 😉
Solução 2: Provavelmente essa forma é a mais intuitiva, mais fácil de visualizar. A esfera não está centrada na origem? Leve a origem a ela então! Como assim? A esfera está deslocada em , não é? Em vez de definirmos , vamos definir , o que nos dá:
É como se você tivesse levado a origem para o ponto . Veja que, substituindo esses valores na equação da esfera, temos:
Temos, agora, uma expressão muito mais simples para a esfera. Talvez voc�� esteja se perguntando: o Jacobiano não muda? Não, porque quando adicionamos ou subtraímos uma constante na mudança de variáveis, a derivada desse termo é zero, logo, o Jacobiano não se altera!
Aqui, vamos optar por essa solução.
Passo 3
Utilizando essa substituição, a região de integração é escrita como:
Exatamente como uma esfera centrada na origem.
Passo 4
Vamos agora escrever o termo em função das novas variáveis.
Montando agora a integral iterada, temos:
Passo 5
Agora integraremos em relação a :
Passo 6
Agora vamos integrar em relação a :
Passo 7
Finalmente, integrando em relação a :