Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3:

Calcule

∭ E   x + y + z d V

sendo a região dentro da superfície x 2 + y 2 + z 2 = 1 no primeiro octante.

Passo 1

A nossa primeira tarefa em problemas de integrais triplas assim é saber quem é a região de integração E assim como descrevê-la da melhor forma possível.

No caso, a região é a esfera de raio 1 , mas no primeiro octante, como você pode ver aqui em baixo :)

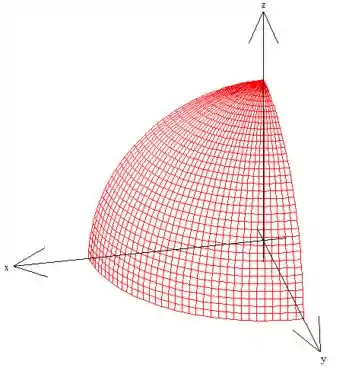
Passo 2

Uma esfera, normalmente nos pede uma mudança para coordenadas esféricas:

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

Não se esqueça do Jacobiano...

J = ρ 2 sin ⁡ φ

Passo 3

Para determinar as variações dos termos dessa nova mudança, ou seja, onde variam ρ ,   φ e θ , basta que saibamos minuciosamente onde esses caras atuam:

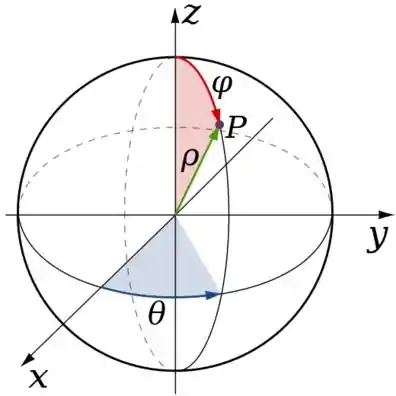
Se compararmos com a nosso sólido E ...

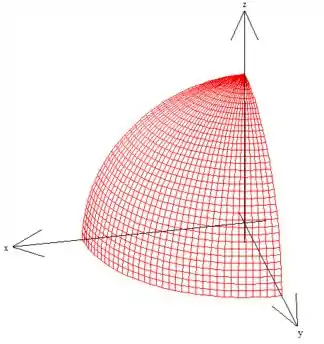
Vamos perceber que ρ é a variação do raio e ela varia da origem, até o raio limite que é o raio da esfera...

0 ≤ ρ ≤ 1

Já o θ , gira de 0 até 90 ° ...

0 ≤ θ ≤ π 2

E o mesmo acontece com o ângulo φ , girando desde lá de cima, até o plano z = 0 ...

0 ≤ φ ≤ π 2

Passo 4

Voltando para a integral que buscamos o valor...

∭ E   x + y + z d V

E já substituindo tudo pelas coordenadas novas não se esquecendo de multiplicar pelo Jacobiano...

∭ E   x + y + z d V = ∫ 0 π 2 ∫ 0 π 2 ∫ 0 1 ρ sin ⁡ φ cos ⁡ θ + ρ sin ⁡ φ sin ⁡ θ + ρ cos ⁡ φ ⋅ J   d r d φ d θ =

∫ 0 π 2 ∫ 0 π 2 ∫ 0 1 ρ 3 sin ⁡ φ cos ⁡ θ + sin ⁡ φ sin ⁡ θ + cos ⁡ φ sin ⁡ φ   d r d φ d θ

Calculando a integral de dentro em ρ , tomando portanto toda a expressão sem ρ constante...

∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin 2 ⁡ φ sin ⁡ θ + sin ⁡ φ cos ⁡ φ ∫ 0 1 ρ 3   d r d φ d θ =

∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin 2 ⁡ φ sin ⁡ θ + sin ⁡ φ cos ⁡ φ ρ 4 4 0 1 d φ d θ =

Substituindo em ρ e lembrando que sin ⁡ 2 φ 2 = sin ⁡ φ cos ⁡ φ ...

1 4 ∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin ⁡ θ + sin ⁡ 2 φ 2 d φ d θ =

1 4 ∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin ⁡ θ d φ d θ + 1 4 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ 2 φ 2 d φ d θ

Vamos então resolver essas duas integrais separados, pois elas exigem coisas diferentes da gente!

Passo 5

Começando coma a que parece mais fácil, ou seja, a segunda...

∫ 0 π 2 ∫ 0 π 2 sin ⁡ 2 φ 2 d φ d θ = 1 2 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ 2 φ d φ d θ =

Integrando...

1 2 ∫ 0 π 2 - cos ⁡ 2 φ 2 0 π 2 d θ = 1 2 ∫ 0 π 2 - cos ⁡ π 2 - - cos ⁡ 0 2 d θ =

1 2 ∫ 0 π 2 1 2 - - 1 2 d θ = 1 2 ∫ 0 π 2 d θ =

1 2 ⋅ π 2 = π 4

Passo 6

Calculando agora a primeira integral dupla lá do passo 4...

∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin ⁡ θ d φ d θ =

Com φ independe de θ , podemos tirar a expressão de dentro da primeira integral...

∫ 0 π 2 cos ⁡ θ + sin ⁡ θ ∫ 0 π 2 sin 2 ⁡ φ d φ d θ =

Lembre-se que...

sin 2 ⁡ φ = 1 - cos ⁡ 2 φ 2

Então...

∫ 0 π 2 cos ⁡ θ + sin ⁡ θ ∫ 0 π 2 1 2 - cos ⁡ 2 φ 2 d φ d θ =

∫ 0 π 2 cos ⁡ θ + sin ⁡ θ 1 2 φ - sin ⁡ 2 φ 4 0 π 2 d θ =

��� 0 π 2 cos ⁡ θ + sin ⁡ θ 1 2 ⋅ π 2 - sin ⁡ π 4 - 1 2 ⋅ 0 - sin ⁡ 0 4 d θ =

Calculando essa expressão dos parênteses e depois integrando em θ ...

∫ 0 π 2 cos ⁡ θ + sin ⁡ θ π 4 d θ = π 4 ∫ 0 π 2 cos �� θ + sin ⁡ θ d θ =

π 4 sin ⁡ θ - cos ⁡ θ 0 π 2 =

π 4 sin ⁡ π 2 - cos ⁡ π 2 - sin ⁡ 0 - cos ⁡ 0 =

π 4 1 - 0 - 0 - 1 = π 2

Passo 7

Voltando para a integral da soma desses dois cara que queremos na realidade do final do passo 4...

∭ E   x + y + z d V = 1 4 ∫ 0 π 2 ∫ 0 π 2 sin 2 ⁡ φ cos ⁡ θ + sin ⁡ θ d φ d θ + 1 4 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ 2 φ 2 d φ d θ

∭ E   x + y + z d V = 1 4 π 2 + 1 4 π 4 = π 8 + π 16 =

3 π 16

Resposta

3 π 16

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ