Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja n , m ∈     0,1 , 2,3 … . Considere:

U = x ,   y ,   z ∈   R 3 ,   x 2 + y 2 + z 2 ≤ 2 , z ≥ 1 .

Considere a integral tripla

I n , m = ∭ U x 2 + y 2 n z m   d x d y d z

  1. Escreva I n , m na forma de uma integral iterada usando coordenadas esféricas ρ ,   ϕ e θ .
  2. Escreva I n , m na forma de uma integral iterada usando as coordenadas cilíndricas r ,   θ , e z .
  3. Calcule I 0,1 ( n = 0 , m = 1 .)

Passo 1

Letra a) Antes de ir partir para a mudança de coordenadas, vem comigo entender essa Região?

Se lembra dessa equação aqui: x 2 + y 2 + z 2 = r 2 ? Ela nos representa uma esfera (menos mal, não é verdade:)?)

Logo, x 2 + y 2 + z 2 ≤ 2 é uma esfera de raio 2 e centrada na origem. Mas note uma coisinha: não estamos interessados apenas na superfície, mas no seu interior também. :D

O sólido U , além de estar dentro dessa esfera, está acima do plano horizontal z = 1 , dessa forma aqui

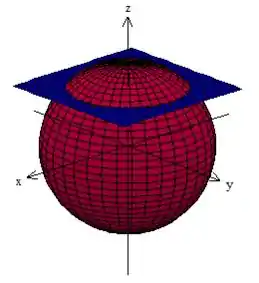
Passo 2

Agora que já sabemos quem é a superfície, podemos partir para a mudança de coordenadas esféricas. Essa daqui, veja

x = ρ sin ⁡ ϕ cos ⁡ θ

y = ρ sin ⁡ ϕ sin ⁡ θ

z = ρ cos ⁡ ϕ

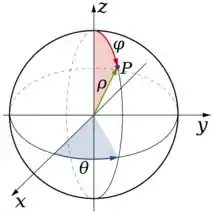
Como estamos realizando uma mudança de coordenadas, necessitaremos do Jacobiano. Se lembra? O Jacobiano da mudança para coordenadas esféricas é

J = ρ 2 sin ⁡ ϕ

Vamos agora então entendermos os limites desses novos caras.

Começando por θ , a gente pode observar que ele tem que dar uma volta completa para gerar o sólido, logo

0 ≤ θ ≤ 2 π

Vamos agora pensar nos limites de ρ . A gente pode observar que ρ está entrando no sólido em baixo no plano e saindo no raio máximo da esfera 2

P l a n o ≤ ρ ≤ 2

lembrando que em coordenadas esféricas, a expressão que associa z é

z = ρ cos ⁡ ϕ   ⇒

como o plano tem equação z = 1 , ganhamos

1 = ρ cos ⁡ ϕ         ⇒         ρ = 1 cos ⁡ ϕ

logo

1 cos ⁡ ϕ ≤ ρ ≤ 2

Quanto a variação de ϕ , podemos notar que ele está variando de 0 até o encontro com o plano z = 1 , onde o raio assume o valor máximo 2 . Logo devemos usar a mesma expressão de z para obter o ângulo máximo, porém não esquecendo de substituir o raio máximo

z = ρ cos ⁡ ϕ

1 = 2 cos ⁡ ϕ →   cos ⁡ ϕ = 1 2 = 2 2

Quem é o ângulo máximo entre 0 e π que dá esse valor para o cosseno? Sim, arccos ⁡ 2 2 = π 4 .

0 ≤ ϕ ≤ π 4

Passo 3

Agora podemos montar a integral: D

I n , m = ∭ U x 2 + y 2 n z m   d x d y d z

I n , m = ∫ 0 2 π ∫ 0 π 4 ∫ 1 cos ⁡ ϕ 2 ρ sin ⁡ ϕ cos ⁡ θ 2 + ρ sin ⁡ ϕ sin ⁡ θ 2 n ρ cos ⁡ ϕ m   J   d ρ d ϕ d θ

só dando uma arrumada nessas contas e simplificando

I n , m = ∫ 0 2 π ∫ 0 π 4 ∫ 1 cos ⁡ ϕ 2 ρ 2 sin 2 ⁡ ϕ ( cos 2 ⁡ θ + sin 2 ⁡ θ ) n ρ cos ⁡ ϕ m   J   d ρ d ϕ d θ

substituindo o Jacobiano, ganharemos por fim

I n , m = ∫ 0 2 π ∫ 0 π 4 ∫ 1 cos ⁡ ϕ 2 ρ 2 sin 2 ⁡ ϕ n ρ cos ⁡ ϕ m   ρ 2 sin ⁡ ϕ d ρ d ϕ d θ

ou ainda, arrumando a casa :D

I n , m = ∫ 0 2 π ∫ 0 π 4 ∫ 1 cos ⁡ ϕ 2 ρ 2 n + m + 2 sin ⁡ ϕ 2 n + 1 cos m ⁡ ϕ d ρ d ϕ d θ

Passo 4

Letra b) Lembrando das coordenadas cilíndricas, teremos

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

o jacobiano dessa mudança é

J = r

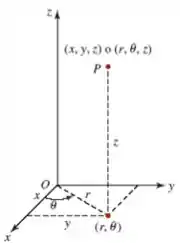
Vamos agora buscar os limites dessas variáveis.

Para os limites de r e θ , vamos olhar para a interação da esfera com o plano z = 1

x 2 + y 2 + z 2 = 2 z = 1         ⇒             x 2 + y 2 = 1

Essa equação que chagamos é a projeção do sólido no plano X Y que é uma circunferência de raio 1 , que é o raio máximo. Como ao raio mínimo é 0 , temos que

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

enquanto isso, temos que z

P l a n o ≤ z ≤ E s f e r a

Sabemos que o plano tem equação z = 1 , já a esfera, temos que trabalhar um pouquinho, veja

z 2 = 2 - ( x 2 + y 2 )

lembrando que x 2 + y 2 = r 2 em coordenadas cilíndricas

z 2 = 2 - r 2

extraindo a raiz e lembrando que apenas queremos a parte positiva de z

z = 2 - r 2  

logo

1 ≤ z ≤ 2 - r 2  

Passo 5

Montando a integral iterada nessas coordenadas, vamos ganhar

I n , m = ∭ U x 2 + y 2 n z m   d x d y d z

I n , m = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2   r 2 n z m J   d z d r d θ

substituindo o jacobiano

I n , m = ∫ 0 2 π ∫ 0 1 �� 1 2 - r 2   r 2 n z m   r   d z d r d θ

I n , m = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2   r 2 n + 1 z m     d z d r d θ

Passo 6

Letra c) Agora chegou a hora de pormos a mão na massa e resolver uma delas tendo I 0,1 . Note como essa segunda, em coordenadas cilíndricas, é bem mais convidativa. Bora resolver por ela?

I 0,1 = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2   r z     d z d r d θ

resolvendo primeiro a integral de dentro

I 0,1 = ∫ 0 2 π ∫ 0 1 r z 2 2 1 2 - r 2   d r d θ

substituindo os limites em z e simplificando

I 0,1 = ∫ 0 2 π ∫ 0 1 r 2 - r 2 2 2 - 1 2 d r d θ

I 0,1 = ∫ 0 2 π ∫ 0 1 r 1 - r 2 2 d r d θ

I 0,1 = ∫ 0 2 π ∫ 0 1 r 2 - r 3 2 d r d θ

indo agora à integral do meio

I 0,1 = ∫ 0 2 π 1 2 ∙ r 2 2 - 1 2 ∙ r 4 4 0 1 d θ = ∫ 0 2 π 1 4 - 1 8 d θ

por fim

I 0,1 = 1 8 ∫ 0 2 π d θ = 1 8 2 π

Resposta

Letra a)

I n , m = ∫ 0 2 π ∫ 0 π 4 ∫ 1 cos ⁡ ϕ 2 ρ 2 n + m + 2 sin ⁡ ϕ 2 n + 1 cos m ⁡ ϕ d ρ d ϕ d θ

Letra b)

I n , m = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2   r 2 n + 1 z m     d z d r d θ

Letra c)

I 0,1 = π 4

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ