Considere a região espacial
E a integral tripla
a) Esboce a região
b) Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas . (Neste item não é pedido o cálculo da integral.)
c) Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas esféricas . (Neste item não é pedido o cálculo da integral.)
d) Calcule .
Passo 1
Resolvendo a letra a) da questão:
Temos uma região limitada por .
A expressão representa a folha superior de um cone com eixo de simetria , de equação geral . Isolando o termo teríamos , como o problema se refere apenas à parte positiva de , sabemos que se trata da folha superior do cone.
Agora vamos analisar e equação . Fazendo o corte , temos uma parábola no plano e fazendo , temos uma parábola no plano . Para cada valor de , temos elipses (no caso, circunferências paralelas a ), temos, portanto, um paraboloide elíptico com eixo de simetria . Como os coeficientes de e de são negativos, a concavidade é para baixo (para o negatvio). O valor máximo de ocorre quando , o que nos dá .
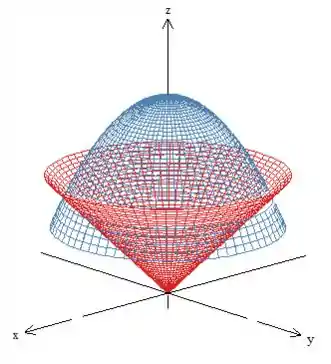
Passo 2
Resolvendo a letra b) da questão:
Para descrever a região em coordenadas cilíndricas, faremos a seguinte substituição nas equações das superfícies:
Para o semicone:
Para o paraboloide:
Pela figura, vemos que os valores de variam entre o semicone e o paraboloide, temos . Vemos, também, que , uma vez que o sólido está envolta do eixo de simetria .
Falta, então, o intervalo de . Veja que essa coordenada varia desde (o eixo ) até onde as duas superfícies se cortam, então, vamos fazer a interseção entre suas equações:
Como o valor de deve ser positivo, temos , o que nos dá:
Passo 3
Reescrevendo a integral em coordenadas cilíndricas, temos, então:
Não se esqueça do fator de conversão .
Passo 4
Resolvendo a letra c) da questão:
Para descrever a região em coordenadas esféricas, faremos a seguinte substituição nas equações das superfícies:
Para o semicone:
Para o paraboloide:
(Lembre-se de que não pode ser negativo).
Agora vamos escrever os intervalos. Pela própria figura, já vemos que , uma vez que o sólido está envolta do eixo de simetria . Os valores de devem variar entre o eixo , onde e a superfície do cone, onde . A coordenada varia desde (na origem) até a superfície do paraboloide, onde é dado pela expressão que acabamos de encontrar acima. Temos, então:
Passo 5
Reescrevendo a integral em coordenadas esféricas, temos:
Não se esqueça do fator de conversão .
Passo 6
Resolvendo a letra d) da questão::
Para resolver a primeira integral, faremos a seguinte substituição:
;
Para a segunda integral, utilizaremos integração por partes:
Fazendo, então, , temos: