Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 851234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848687888990919293949596979899100

Enunciado

Questão 3: Use coordenadas esféricas para calcular o volume do sólido S que está dentro da esfera x 2 + y 2 + z 2 = 9 , acima do plano x y e abaixo do cone z 2 = 3 x 2 + y 2 .

Passo 1

Cara! Calculo de volume a esse altura do campeonato pra gente é uma integral tripla de 1 :

∭ W   1   d V

Não temos uma boa visualização desse sólido W por isso sempre é bom começar por aqui . Mas relaxa, pois fazer isso nada mais é do que desenhar todas essas superfícies aí ao mesmo tempo! Quando fazemos isso, a superfície que ganhamos no espaço é esta daqui, oh:

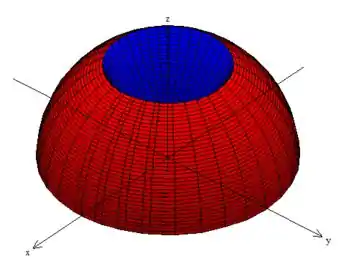
Pegou? :D

Passo 2

Bem, estamos trabalhando dentro de uma esfera, então... Nada mais justo utilizarmos as coordenadas esféricas, onde

x = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

z = r cos ⁡ φ                    

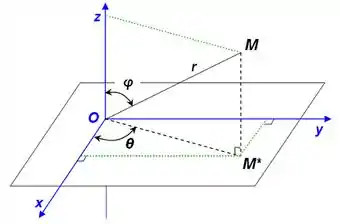
O jacobiano dessa mudança é

J = r 2 sin ⁡ φ              

Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?

Passo 3

Bem, vamos começar aqui falando da variação do mais fácil... Do próprio raio r : ora, sabemos que ele está saindo da origem e está indo até o raio máximo que é o raio da esfera vermelha:

0 ≤ r ≤ 3

Quanto ao ângulo θ , bem ele está dando uma volta completa, neh?! Então...

0 ≤ θ ≤ 2 π

Já o φ ... Bem, se você olhar mais atentamente o sólido

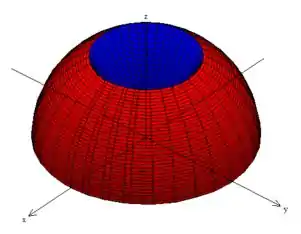
vai perceber que esse ângulo está entrando pelo cone e está saindo no ângulo reto

C o n e   A z u l ≤ φ ≤ π 2

O C o n e   A z u l tem equação z 2 = 3 x 2 + y 2 . Epa! Estamos trabalhando com as coordenadas polares, então devemos substitui-las nessas equações, veja

z = 3 x 2 + y 2                   →                           r cos ⁡ φ = 3 r sin ⁡ φ cos ⁡ θ 2 + r sin ⁡ φ sin ⁡ θ 2                     →

      r cos ⁡ φ = 3 r 2 sin 2 ⁡ φ cos 2 ⁡ θ + r 2 sin 2 ⁡ φ sin 2 ⁡ θ                         →

    r cos ⁡ φ = 3 r 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ = 3 r 2 sin 2 ⁡ φ

Como o seno é positivo e o raio também...

r cos ⁡ φ = 3   r sin ⁡ φ     →         1 ∙   r cos ⁡ φ = 3   r sin ⁡ φ

passando esse r cos  ⁡ φ pro outro lado dividindo...

r sin ⁡ φ r cos ⁡ φ = 1 3           →           tan ⁡ φ = 1 3

Nessas condições, φ = 30 ° = π 6

logo

π 6 ≤ φ ≤ π 2

Passo 4

Bem, agora é só montar a integral tripla e correr para o abraço!

∭ W   d V

Substituindo as variações e trocando para coordenadas cilíndricas não se esquecendo de multiplicar pelo J a c o b i a n o ...

∫ 0 2 π ∫ π 6 π 2 ∫ 0 3 J   d r d φ d θ =

∫ 0 2 π ∫ π 6 π 2 ∫ 0 3 r 2 sin ⁡ φ   d r d φ d θ =

Resolvendo a integral de dentro...

∫ 0 2 π ∫ π 6 π 2 sin ⁡ φ ∫ 0 3 r 2   d r d φ d θ =

∫ 0 2 π ∫ π 6 π 2 sin ⁡ φ r 3 3 0 3 d φ d θ =

depois a do meio

9 ∫ 0 2 π ∫ π 6 π 2 sin ⁡ φ d φ d θ =

9 ∫ 0 2 π ∫ π 6 π 2 sin ⁡ φ d φ d θ =

9 ∫ 0 2 π - cos ⁡ φ π 6 π 2 d θ =

9 ∫ 0 2 π - cos ⁡ π 2 - - cos ⁡ π 6 d θ =

Em seguida a última, chegamos à...

9 ∫ 0 2 π 3 2 d θ = 9 3 π

Resposta

9 3 π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ