Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 771234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757678798081828384858687888990919293949596979899100

Enunciado

UFRJ. Cálculo 3. PF. 2022.1. Questão 2.

Calcule a integral tripla

∫ ∫ ∫ W z 2 d V

onde W = x , y , z ∈ R 3 :   x 2 + y 2 + z 2 ≤ 16 ,   x 2 + y 2 + z 2 ≥ 4 z   e   0 ≤ z ≤ x 2 + y 2 3 .

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão temos uma integral tripla de z 2 onde a região de integração é dada pela região W .

Essa região é limitada superiormente pela esfera pela esfera x 2 + y 2 + z 2 = 16 excluindo a esfera x 2 + y 2 + z 2 = 4 z , abaixo da superfície z = x 2 + y 2 3 e acima de z = 0 .

Muita informação, não é? 👀

Primeiro vamos ver como é a região limitada pelas esferas.

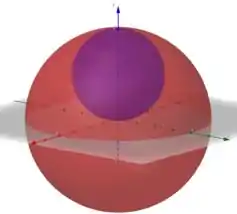
A esfera vermelha é obtida pela equação x 2 + y 2 + z 2 = 16 e a roxa pela equação x 2 + y 2 + z 2 = 4 z . Como o centro delas estão em pontos diferentes, temos que calcular a integral da esfera vermelha e subtrair a integral da esfera roxa.

Entendeu? 👀

Passo 2

Analisando os limites em z para z = 0 e z = x 2 + y 2 3 , temos

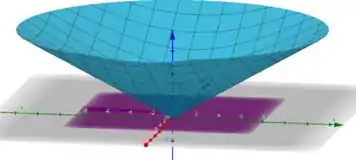
A área que queremos está abaixo de z = x 2 + y 2 3 e acima de z = 0 .

Como W é limitada por esferas, vamos usar coordenadas esféricas para resolver essa integral.

Lembra como fazemos a mudança de coordenadas retangulares para coordenadas esféricas?

x = ρ s e n ϕ cos ⁡ θ y = ρ s e n ϕ sen ⁡ θ z = ρ cos ⁡ ϕ

Como dito anteriormente, vamos dividir em duas integrais, onde para a esfera vermelha vamos ter a região S 1 e para a esfera roxa vamos ter a região S 2 , ou seja

∫ ∫ ∫ W z 2 d V = ∫ ∫ ∫ S 1 z 2 d V - ∫ ∫ ∫ S 2 z 2 d V

Vamos definir as integrais de S 1 e de S 2 .

Para S 1 as variáveis ρ , ϕ e θ , vão ser:

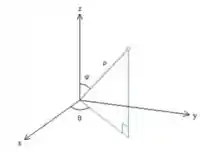
ρ é o raio da esfera, como sua equação é x 2 + y 2 + z 2 = 16 , vemos que ρ 2 = 16 , ou seja, ρ = 4 .

ϕ é a variação do ângulo que nossa região faz com o eixo z positivo.

Como vemos no gráfico de z = x 2 + y 2 3 e z = 0 , a variação angular que essas superfícies fazem com z + é ϕ = a r c t g C a t e t o   O p o s t o C a t e t o   A d j e c e n t e , ou seja, ϕ = a r c t g x 2 + y 2 z

Se z = x 2 + y 2 3 e a b = a b , então

ϕ = a r c t g x 2 + y 2 x 2 + y 2 3 = a r c t g x 2 + y 2 x 2 + y 2 3

Simplificando...

ϕ = a r c t g 3 = π 3

E como o limite inferior é um ângulo de 90 ° então

π 3 ≤ ϕ ≤ π 2

Já θ é a variação do ângulo que a região faz com o semieixo positivo x , ou seja, 0 ≤ θ ≤ 2 π .

Com isso, lembrando que o jacobiano dessa transformação é ρ 2 s e n ϕ e que z 2 = ρ 2 cos 2 ⁡ ϕ em coordenadas esférica, a integral de S 1 será

∫ 0 2 π ∫ π 3 π 2 ∫ 0 4 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ d ϕ d θ

Tranquilo até aqui? 😁

Passo 3

Agora vamos calcular a integral de S 2 .

Nesse caso, ϕ e θ vão ser os mesmos, já ρ vai ser obtido na sua equação

x 2 + y 2 + z 2 = 4 z

Se x 2 + y 2 + z 2 = ρ 2 e z = ρ cos ⁡ ϕ , temos

ρ 2 = 4 ρ cos ⁡ ϕ

Simplificando ρ .

ρ = 4 cos ⁡ ϕ

Com isso, a integral de S 2 é

∫ 0 2 π ∫ π 3 π 2 ∫ 0 4 cos ⁡ ϕ ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ d ϕ d θ

Calculando a integral com relação a ρ pelo método de integração polinomial

∫ ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = ρ 4 + 1 4 + 1 cos 2 ⁡ ϕ s e n ϕ = ρ 5 5 cos 2 ⁡ ϕ s e n ϕ

Aplicando os limites de integração em S 1

∫ 0 4 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 4 5 5 cos 2 ⁡ ϕ s e n ϕ - 0 5 5 cos 2 ⁡ ϕ s e n ϕ

∫ 0 4 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 1024 5 cos 2 ⁡ ϕ s e n ϕ

Agora para S 2 , vamos ter

∫ 0 4 cos ⁡ ϕ ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 4 cos ⁡ ϕ 5 5 cos 2 ⁡ ϕ s e n ϕ - 0 5 5 cos 2 ⁡ ϕ s e n ϕ

∫ 0 4 cos ⁡ ϕ ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 1024 5 cos 7 ⁡ ϕ s e n ϕ

Agora com base nesses resultados, partimos para dois caminhos diferentes.

Entendeu até aqui?

Passo 4

Vamos continuar o cálculo da superfície S 1 integrando o resultado da primeira integral dessa vez com relação a ϕ

∫ 1024 5 cos 2 ⁡ ϕ s e n ϕ d ϕ

Se fizermos cos ⁡ ϕ = u , d u = - s e n ϕ , assim podemos aplicar o método da substituição nessa integral

∫ - 1024 5 u 2 d u = - 1024 5 u 2 + 1 2 + 1 = - 1024 5 u 3 3

Voltando u para cos ⁡ ϕ

∫ 1024 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = - 1024 c o s 3 ϕ 15

Aplicando os limites de integração

∫ π 3 π 2 1024 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = - 1024 c o s 3 π 2 15 - - 1024 c o s 3 π 3 15

∫ π 3 π 2 1024 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = 128 15

Integrando esse resultado com relação a θ

∫ 128 15 d θ

Como nossa função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.

∫ 128 15 d θ = 128 15 θ

Aplicando os limites de integração

∫ 0 2 π 128 15   d θ = 128 15 2 π - 128 15 0

∫ 0 2 π 128 15   d θ = 256 π 15

Com isso, obtemos a integral de S 1

∫ 0 2 π ∫ π 4 π 2 ∫ 0 4 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ d ϕ d θ = 256 π 15

Tudo certo até aqui?

Passo 5

Agora vamos completar a integral de S 2 integrando o resultado que tínhamos obtido com relação a ϕ , temos

∫ 1024 5 cos 7 ⁡ ϕ s e n ϕ d ϕ

Se fizermos cos ⁡ ϕ como u , d u = - s e n ϕ e então podemos aplicar o método de integração por substituição.

∫ - 1024 5 u 7 d ϕ

Integrando pelo método de integração polinomial

∫ - 1024 5 u 7 d ϕ = - 1024 5 u 7 + 1 7 + 1 = - 1024 u 8 40

Voltando u para cos ⁡ ϕ

∫ 1024 5 cos 7 ⁡ ϕ s e n ϕ d ϕ = - 1024 cos 8 ⁡ ϕ 40

Aplicando os limites de integração.

∫ π 3 π 2 1024 5 cos 7 ⁡ ϕ s e n ϕ d ϕ = - 1024 cos 8 ⁡ π 2 40 - - 1024 cos 8 ⁡ π 3 40

∫ π 3 π 2 1024 5 cos 7 ⁡ ϕ s e n ϕ d ϕ = 1 10

Integrando esse resultado com relação a θ

∫ 0 2 π 1 10 d θ

Como nossa função de integração é uma constante, podemos aplicar a mesma ideia da anterior.

∫ 1 10 d θ = 1 10 θ

Aplicando os limites de integração.

∫ 0 2 π 1 10 d θ = 1 10 2 π - 1 10 0 = π 5

Logo a integral de S 2 é

∫ 0 2 π ∫ π 4 π 2 ∫ 0 4 cos ⁡ ϕ ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ d ϕ d θ = π 5

Interessante, não é? 😎

Passo 6

Como dizemos no começo do nosso problema, a integral que buscamos é a diferença entre a integral de S 1 e a integral de S 2

∫ ∫ ∫ W z 2 d V = ∫ ∫ ∫ S 1 z 2 d V - ∫ ∫ ∫ S 2 z 2 d V

Como obtemos

∫ ∫ ∫ S 1 z 2 d V = 256 π 15 ,     ∫ ∫ ∫ S 2 z 2 d V = π 5

Ou seja

∫ ∫ ∫ W z 2 d V = 256 π 15 - π 5 = 256 π 15 - 3 π 1 5

Ou seja, nossa integral de z 2 em W é

∫ ∫ ∫ W z 2 d V = 253 π 15

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

∫ ∫ ∫ W z 2 d V = 253 π 15

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ