Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 571234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

4. Considere o sólido E correspondente à parte dentro do cone z = x 2 + y 2   que está dentro da esfera x 2 + y 2 + z 2 = 1

  1. Esboce E
  2. Calcule a integral.

∭ E   z 2   d x d y d z

Passo 1

  1. Oi, galerinha! Tudo bom? Aqui temos uma região E para esboçar. O problema já nos informou que temos um cone cuja a equação é

    2. z = x 2 + y 2

    Ou seja, ele estará ao longo do eixo z . Mas o problema, nos deu outra informação, disse que ele é limitado pela esfera x 2 + y 2 + z 2 = 1 , ou seja, vamos ter que desenhar uma esfera de raio 1 também.

    Fazendo os dois esboços, ficamos com:

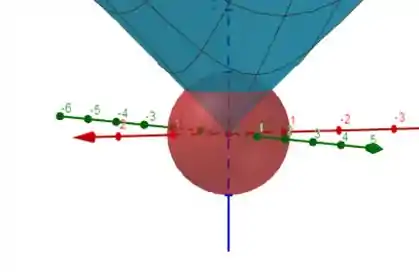
    Repara que o cone azul corta a nossa esfera vermelha,formando uma região E cuja a base inferior é limitada pelo cone azul e a parte superior é limitada pela esfera.

    Passo 2

  2. Agora temos que calcular

∭ E   z 2   d x d y d z

Repara que temos que integrar z 2 . Pelo esboço que fizemos no passo anterior, vamos encontrar os limites de integração! Mas como a região é limitada por duas esferas e um cone, vamos utilizar coordenadas esféricas:

x = ρ   s e n   φ   c o s   θ

y = ρ   s e n   φ   s e n   θ

z = ρ cos ⁡ φ

J = ρ 2 s e n   φ

Agora Precisamos agora escrever matematicamente a região de integração. Pela própria figura, já temos que 0 ≤ θ ≤ 2 π (uma volta completa em torno de z ). Os valores de ρ variam desde a superfície do cone (parte inferior) até a esfera (parte superior). O cone, como está centrado na origem, pode ser escrita como ρ = 0 . Precisamos, então, fazer a mudança de coordenadas na equação da esfera:

ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2 + ρ cos ⁡ φ 2 = 1

ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ = 1

ρ 2 s e n 2 φ   + ρ 2 cos 2 ⁡ φ = 1

ρ = 1

Temos, então 0 ≤ ρ ≤ 1 .

Falta agora o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , onde temos φ = 0 até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:

ρ cos ⁡ φ = ρ   s e n   φ   c o s   θ 2 + ρ   s e n   φ   s e n   θ 2

ρ cos ⁡ φ = ρ 2 s e n 2 φ cos 2 ⁡ θ + ( ρ 2 s e n 2 φ )   s e n 2 θ

ρ cos ⁡ φ = ρ 2 s e n 2 φ   = ρ   s e n   φ

s e n   φ = cos ⁡ φ   → t g   φ = 1     →   φ = π / 4

Portanto, 0 ≤ φ ≤ π / 4 .

Passo 2

Vamos agora substituir os intervalos que encontramos na integral iterada (não esquecendo de multiplicar pelo Jacobiano):

∫ 0 π / 4 ∫ 0 2 π ∫ 0 1 ρ cos ⁡ φ 2 ρ 2 s e n   φ   d ρ   d θ   d φ =

= ∫ 0 π / 4 ∫ 0 2 π ∫ 0 1 ρ 4 cos 2 ⁡ φ s e n   φ   d ρ   d θ   d φ =

Passo 3

Agora integraremos em relação a ρ :

= ∫ 0 π / 4 ∫ 0 2 π ρ 5 5 cos 2 ⁡ φ s e n   φ ρ = 0 ρ = 1   d θ   d φ =

= 1 5 ∫ 0 π / 4 ∫ 0 2 π cos 2 ⁡ φ s e n   φ   d θ   d φ =

Passo 4

Agora vamos integrar em relação a θ :

= 1 5 ∫ 0 π / 4 ( cos 2 ⁡ φ s e n   φ ) θ θ = 0 θ = 2 π   d φ =

= 2 π 5 ∫ 0 π / 4 cos 2 ⁡ φ s e n   φ   d φ =

Passo 5

Vamos calcular a integral:

cos 2 ⁡ φ = u

- 2 s e n   φ cos 2 ⁡ φ d φ = d u

cos ⁡ 0 = 1   → u = 1

cos ⁡ π / 4 = 2 2 → u = 1 / 16

2 π 5 ∫ 0 π / 4 cos 2 ⁡ φ s e n   φ   d φ = 2 π 5 ∫ 1 1 / 16 - 1 2 d u =

= - π 5 u 1 1 16 = - π 5 1 16 - 1 = - π 5 - 15 16

= 3 π 16

Resposta

3 π 16

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ