O valor da integral
é:
Passo 1
Bom, logo de cara, se você for observar, calcular essa integral nesse intervalo com raízes e tal, ia ser algo bem complicado. Uma coisa que sugere a mudança de variáveis ´f na nossa termos oque logo de cara nos lembra das coordenadas esféricas.
Passo 2
Observa o que temos ainda dessa questão:
Trabalhando com 1)
Opa, com isso aí da pra perceber que estamos trabalhando dentro da esfera de raio 2. Detalhe, observa que inicialmente tínhamos a raíz (POSITIVA) isolada do lado direito, certo? Isso significa que só estamos trabalhando com a parte superior (Z POSITIVO) da esfera.
Passo 3
Trabalhando agora com 2)
Daí da pra ver que estamos trabalhando com uma circonferência de raio 2 (no prano xy). Detalhe, da mesma forma que no passo anterior, observar que so estamos andando no y positivo.
Detalhe ainda que temos o x variando entre 0 e 2, ou seja, somente x positivo!
Passo 4
Depois desses passos é possível observar que estamos trabalhando somente com da esfera total.
Lembra como variam os parâmetros?
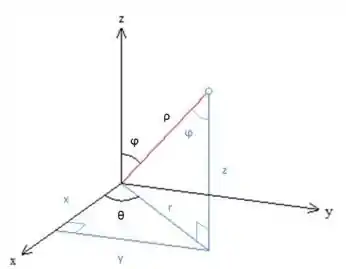
Como estamos trabalhando só na parte superior da esfera,
O que parte de x positivo, vai até o eixo x negativo, uma vez que só queremos a região do x e y positivo.
E pra fechar ficamos com a variação do raio sendo bem simples
Passo 5
Vamos então escrever nossa integral (sem esquecer o jacobiano):