Questão discursiva – UFJF - calculo 3 – lista de estudos – questão 4 item b
Seja o sólido interior ao cone abaixo do plano e considere a integral
b) forneça uma expressão para em coordenadas esféricas.
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O problema nos pede para calcularmos o volume delimitadoa por um sólidosolido interno a um cone (o próprio cone) dado pelas equações:
Calcularmos isso em coordenadas esféricas. Que tal vermos como essa região é?
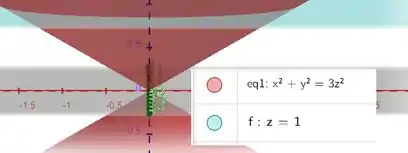
É essa região cônica vermelha.
E bom, é pedido para fazermos essa integral por coordenadas esféricas. Como elas são?
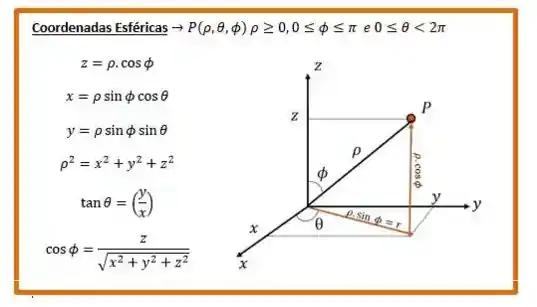
E com elas conseguimos obter a nossa transformação de coordenadas cartesianas para coordenadas esféricas.
Mas a vida seria muito fácil se pudéssemos trocar as coordenadas assim, e ela é? Nesse caso não hashua. Para que possamos trocar coordenadas, há um fator chamado de jacobiano , ele que permite que olhemos um problema em uma coordenada para outra sem perda de generalidade.
Então ok, resumindo temos que achar o jacobiano das coordenadas esféricas, achar os limites de integração e achar a função em coordenadas esféricas. Bora lá?
Bora pro próximo passo?!
Passo 2
Vamos achar o jacobiano das coordenadas esféricas. Como ele é calculado?
Realizando as derivadas, temos:
Achando o determinante, vemos que:
E achamos então o Jacobiano das coordenadas esféricas.
Passo 3
Obrigado por vir.
Vamos então achar os limites de integração de e das coordenadas esféricas?
Primeiramente vemos, de acordo com a imagem do Volume, que o ângulo é completo, ou seja, roda até , assim:
E ? Bom, temos a equação , e como sabemos, o ângulo é o ângulo entre o eixo e a função, que nesse caso é . OK, então:
Somando em ambos os lados:
Sabemos que , logo:
Substituindo
Dividindo por e isolando
Logo vemos que:
Assim:
E por fim, para . Achamos na determinação de que:
Logo:
Mas pela segunda equação que limita o crescimento do nosso volume, temos , logo:
Mas o que era ?
Pois nesse caso então cresce de acordo com o ângulo. Assim:
Resumindo:
Agora vamos achar a nossa função em coordenadas esféricas?
Passo 4
Temos então:
Temos que fazer. Para isso, sabemos que:
Logo:
Que é:
Podemos fatorar né?
Usando que e tirando a raiz de :
E achamos então a nossa função em coordenadas esféricas.
Parece que já temos tudo então, vamos para a integração
Passo 5
Assim, temos:
Substituindo :
Integrando em
Vemos que:
Logo:
Façamos aqui uma substituição. Seja:
Logo:
E além disso:
Assim, substituindo:
Cortando e integrando em :
Logo:
Integrando em :
Portanto:
E achamos então o nosso resultado.
E olha que bacana! Acharíamos o mesmo resultado se tivesse feito tanto pelas coordenadas cartesianas quanto pelas cilíndricas que achamos no item a)
Legal, né?! Te convido a tentar, te espero na próxima! Até lá.