Calcule a integral tripla
Passo 1
Observa que temos
Isso basicamente é a parte interior de raio 1 no primeiro octante. Como que eu vi isso?
Observa primeiro que z varia entre 0 e uma função. Que função é essa?
Isso é basicamente uma esfera de raio 1! No entanto, observa que como a raíz era positiva, queremos só a parte de z positivo!
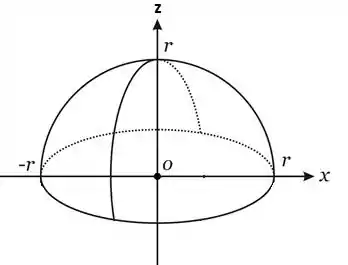
Temos ainda que varia entre 0 e
Notou a circunferência? Mais uma vez, somente a parte positiva da circuntefencia, logo
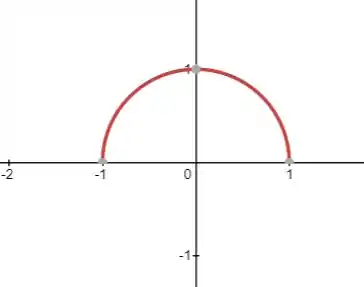
Se você for observar, isso nos limita ao primeiro octante, ou seja, onde x, y e z são positivos (lembrando que x varia entre 0 e 1).
Passo 2
Já que estamos trabalhando com uma esfera pensamos em que? Você está certo se pensou em mudança para coordenadas esféricas haha.
Teremos
Sem esquecer o Jacobiano

Passo 3
Substituindo na noss integral temos
Lembrando que
Pois estamos trabalhando somente no primeiro octante.
Agora é solresolver a integral.