Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 761234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757778798081828384858687888990919293949596979899100

Enunciado

Coordenadas esféricas

Calcule a integral tripla ∭ H   9 - x 2 - y 2 d V , em que H é o hemisfério sólido x 2 + y 2 + z 2 ≤ 9 acima do plano x y .

Passo 1

Bom, vamos começar esboçando a região de integração. Temos uma esfera de raio 3 centrada na origem cortada pelo plano x y :

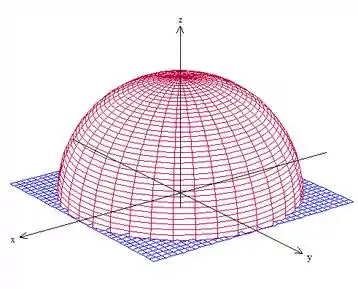
Passo 2

Como a região é limitada por uma esfera e um plano, vamos utilizar coordenadas esféricas:

x = ρ sen ⁡ φ c o s   θ

y = ρ   sen ⁡ φ sen ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sen ⁡ φ

Passo 3

Precisamos escrever matematicamente a região de integração.

Pela própria figura, já vemos que 0 ≤ θ ≤ 2 π , pois o sólido está envolta do eixo z ,fazendo uma volta completa. Os valores de ρ , nós vemos que variam desde a origem ρ = 0 até a superfície da esfera de raio 3 , que pode ser escrita como ρ = 3 .

Temos, então, 0 ≤ ρ ≤ 3

Falta, então, o intervalo de φ . Pela figura, vemos que esse ângulo varia desde o eixo z , quando φ = 0 até a superfície do plano, onde φ = π / 2 .

Portanto, 0 ≤ φ ≤ π / 2 . A região será escrita como:

W = { ( ρ , θ , φ ) | 0 ≤ φ ≤ π / 2 ; 0 ≤ θ ≤ 2 π ;   0 ≤ ρ ≤ 3   }

Passo 4

Vamos agora substituir os intervalos que encontramos na integral iterada.

∭ H   9 - x 2 - y 2 d V

= ∫ 0 π / 2 ∫ 0 2 π ∫ 0 3 9 - ρ sen ⁡ φ c o s   θ 2 - ρ   sen ⁡ φ sen ⁡ θ 2 ρ 2 sen ⁡ φ d ρ   d θ   d φ =

= ∫ 0 π / 2 ∫ 0 2 π ∫ 0 3 9 - ρ 2 sen 2 ⁡ φ ρ 2 sen ⁡ φ d ρ   d θ   d φ =

= ∫ 0 π / 2 ∫ 0 2 π ∫ 0 3 9 ρ 2 sen ⁡ φ - ρ 4 sen 3 ⁡ φ d ρ   d θ   d φ =

Passo 5

Agora integraremos em relação a ρ :

= ∫ 0 π / 2 ∫ 0 2 π 3 ρ 3 sen ⁡ φ - ρ 5 5 sen 3 ⁡ φ 0 3   d θ   d φ =

= ∫ 0 π / 2 ∫ 0 2 π 81 sen ⁡ φ - 243 5 sen 3 ⁡ φ   d θ   d φ =

Integramos então em relação a θ : = ∫ 0 π / 2 81 sen ⁡ φ - 243 5 sen 3 ⁡ φ 0 2 π     d φ =

= 2 π ∫ 0 π / 2 81 sen ⁡ φ - 243 5 sen 3 ⁡ φ     d φ =

Finalmente, em relação a φ . Vamos reescrever, primeiro, essa integral:

= 2 π ∫ 0 π / 2 81 sen ⁡ φ - 243 5 sen ⁡ φ sen 2 ⁡ φ     d φ =

= 2 π ∫ 0 π / 2 81 sen ⁡ φ - 243 5 sen ⁡ φ 1 - cos 2 ⁡ φ     d φ =

= 162 π ∫ 0 π / 2 sen ⁡ φ     d φ - 486 π 5 ∫ 0 π / 2 sen ⁡ φ 1 - cos 2 ⁡ φ     d φ =

= 162 π ∫ 0 π / 2 sen ⁡ φ     d φ - 486 π 5 ∫ 0 π 2 sen ⁡ φ d φ + 486 π 5   ∫ 0 π / 2 sen ⁡ φ cos 2 ⁡ φ     d φ =

= 324 π 5 ∫ 0 π / 2 sen ⁡ φ     d φ + 486 π 5   ∫ 0 π / 2 sen ⁡ φ cos 2 ⁡ φ     d φ =

A primeira integral é tranquila:

= - 324 π 5  cos ⁡ φ 0 π 2     d φ + 486 π 5   ∫ 0 π / 2 sen ⁡ φ cos 2 ⁡ φ     d φ =

= 324 π 5   + 486 π 5   ∫ 0 π / 2 sen ⁡ φ cos 2 ⁡ φ     d φ =

Agora, como:

d cos 3 ⁡ φ d φ = - 3 sen ⁡ φ cos 2 ⁡ φ

∫ sen ⁡ φ cos 2 ⁡ φ   d φ = - 1 3 cos 3 ⁡ φ

Temos então:

= = 324 π 5 - 162 π 5 cos 3 ⁡ φ 0 π / 2 =

= 324 π 5 + 162 π 5 =

= 486 π 5

Resposta

486 π 5

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ